
HL Paper 2
A particular K meson has a quark structure s. State the charge, strangeness and baryon number for this meson.
The Feynman diagram shows the changes that occur during beta minus (β–) decay.
Label the diagram by inserting the four missing particle symbols and the direction of the arrows for the decay particles.
C-14 decay is used to estimate the age of an old dead tree. The activity of C-14 in the dead tree is determined to have fallen to 21% of its original value. C-14 has a half-life of 5700 years.
(i) Explain why the activity of C-14 in the dead tree decreases with time.
(ii) Calculate, in years, the age of the dead tree. Give your answer to an appropriate number of significant figures.
Markscheme
charge: –1«e» or negative or K−
strangeness: –1
baryon number: 0
Negative signs required.
Award [2] for three correct answers, [1 max] for two correct answer and [0] for one correct answer.
correct symbols for both missing quarks
exchange particle and electron labelled W or W– and e or e–
Do not allow W+ or e+ or β+. Allow β or β–.
arrows for both electron and anti-neutrino correct
Allow ECF from previous marking point.
i
number of C-14 atoms/nuclei are decreasing
OR
decreasing activity proportional to number of C-14 atoms/nuclei
OR
A = A0e–λt so A decreases as t increases
Do not allow “particles”
Must see reference to atoms or nuclei or an equation, just “C-14 is decreasing” is not enough.
ii
0.21 = (0.5)n
OR
n = 2.252 half-lives or t =1 2834 «y»
Early rounding to 2.25 gives 12825 y
13000 y rounded correctly to two significant figures:
Both needed; answer must be in year for MP3.
Allow ECF from MP2.
Award [3] for a bald correct answer.
Examiners report
Plutonium-238 (Pu) decays by alpha (α) decay into uranium (U).
The following data are available for binding energies per nucleon:
plutonium 7.568 MeV
uranium 7.600 MeV
alpha particle 7.074 MeV
The energy in b(i) can be transferred into electrical energy to run the instruments of a spacecraft. A spacecraft carries 33 kg of pure plutonium-238 at launch. The decay constant of plutonium is 2.50 × 10−10 s−1.
Solar radiation falls onto a metallic surface carried by the spacecraft causing the emission of photoelectrons. The radiation has passed through a filter so it is monochromatic. The spacecraft is moving away from the Sun.
State what is meant by the binding energy of a nucleus.
Draw, on the axes, a graph to show the variation with nucleon number of the binding energy per nucleon, . Numbers are not required on the vertical axis.
Identify, with a cross, on the graph in (a)(ii), the region of greatest stability.
Some unstable nuclei have many more neutrons than protons. Suggest the likely decay for these nuclei.
Show that the energy released in this decay is about 6 MeV.
The plutonium nucleus is at rest when it decays.
Calculate the ratio .
Estimate the power, in kW, that is available from the plutonium at launch.
The spacecraft will take 7.2 years (2.3 × 108 s) to reach a planet in the solar system. Estimate the power available to the spacecraft when it gets to the planet.
State and explain what happens to the kinetic energy of an emitted photoelectron.
State and explain what happens to the rate at which charge leaves the metallic surface.
Markscheme
the energy needed to «completely» separate the nucleons of a nucleus
OR
the energy released when a nucleus is assembled from its constituent nucleons ✓
Accept reference to protons and neutrons.
curve rising to a maximum between 50 and 100 ✓
curve continued and decreasing ✓
Ignore starting point.
Ignore maximum at alpha particle.
At a point on the peak of their graph ✓
beta minus «decay» ✓
correct mass numbers for uranium (234) and alpha (4) ✓
«MeV» ✓
energy released 5.51 «MeV» ✓
Ignore any negative sign.
«» OR ✓
«» ✓
Award [2] marks for a bald correct answer.
Accept for MP2.
number of nuclei present ✓
initial activity is ✓
power is «kW» ✓
Allow a final answer of 20 kW if 6 MeV used.
Allow ECF from MP1 and MP2.
available power after time t is ✓
«kW» ✓
MP1 may be implicit.
Allow ECF from (c)(i).
Allow 17.4 kW from unrounded power from (c)(i).
Allow 18.8 kW from 6 MeV.
stays the same ✓
as energy depends on the frequency of light ✓
Allow reference to wavelength for MP2.
Award MP2 only to answers stating that KE decreases due to Doppler effect.
decreases ✓
as number of photons incident decreases ✓
Examiners report
One possible fission reaction of uranium-235 (U-235) is
Mass of one atom of U-235
Binding energy per nucleon for U-235
Binding energy per nucleon for Xe-140
Binding energy per nucleon for Sr-94
A nuclear power station uses U-235 as fuel. Assume that every fission reaction of U-235 gives rise to of energy.
A sample of waste produced by the reactor contains of strontium-94 (Sr-94). Sr-94 is radioactive and undergoes beta-minus () decay into a daughter nuclide X. The reaction for this decay is
.
The graph shows the variation with time of the mass of Sr-94 remaining in the sample.
State what is meant by binding energy of a nucleus.
Outline why quantities such as atomic mass and nuclear binding energy are often expressed in non-SI units.
Show that the energy released in the reaction is about .
Estimate, in , the specific energy of U-235.
The power station has a useful power output of and an efficiency of . Determine the mass of U-235 that undergoes fission in one day.
The specific energy of fossil fuel is typically . Suggest, with reference to your answer to (b)(i), one advantage of U-235 compared with fossil fuels in a power station.
Write down the proton number of nuclide X.
State the half-life of Sr-94.
Calculate the mass of Sr-94 remaining in the sample after minutes.
Markscheme
energy required to «completely» separate the nucleons
OR
energy released when a nucleus is formed from its constituent nucleons ✓
Allow protons AND neutrons.
the values «in SI units» would be very small ✓
OR ✓
see AND ✓
✓
energy produced in one day ✓
mass ✓
«specific energy of uranium is much greater than that of coal, hence» more energy can be produced from the same mass of fuel / per
OR
less fuel can be used to create the same amount of energy ✓
✓
Do not allow unless the proton number is indicated.
✓
ALTERNATIVE 1
✓
mass remaining ✓
ALTERNATIVE 2
decay constant ✓
mass remaining ✓
Examiners report
Generally, well answered but candidates did miss the mark by discussing the constituents of a nucleus rather than the nucleons, or protons and neutrons. There seemed to be fewer comments than usual about 'the energy required to bind the nucleus together'.
Well answered with some candidates describing the values as too large or small.
Well answered.
This caused problems for some with mass often correctly calculated but energy causing more difficulty with the eV conversion either being inaccurate or omitted. Candidates were allowed error carried forward for the second mark as long as they were dividing an energy by a mass.
Most candidates had the right idea, but common problems included forgetting the efficiency or not converting to days.
HL only. This was well answered.
Most candidates answered this correctly.
Most candidates answered this correctly.
This was answered well with most candidates (even at HL) going down the number of half-lives route rather than the exponential calculation route.
Radioactive uranium-238 produces a series of decays ending with a stable nuclide of lead. The nuclides in the series decay by either alpha (α) or beta-minus (β−) processes.
The graph shows the variation with the nucleon number A of the binding energy per nucleon.
Uranium-238 decays into a nuclide of thorium-234 (Th).
Write down the complete equation for this radioactive decay.
Thallium-206 decays into lead-206 .
Identify the quark changes for this decay.
The half-life of uranium-238 is about 4.5 × 109 years. The half-life of thallium-206 is about 4.2 minutes.
Compare and contrast the methods to measure these half-lives.
Outline why high temperatures are required for fusion to occur.
Outline, with reference to the graph, why energy is released both in fusion and in fission.
Uranium-235 is used as a nuclear fuel. The fission of uranium-235 can produce krypton-89 and barium-144.
Determine, in MeV and using the graph, the energy released by this fission.
Markscheme
✓
Allow He for alpha.
udd→uud
OR
down quark changes to up quark ✓
measure «radio»activity/«radioactive» decay/A for either
OR
take measurements with a Geiger counter. ✓
for Uranium measure number/N of radioactive atoms/OWTTE ✓
for Thalium measure «rate of» change in activity over time. ✓
correct connection for either Uranium or Thalium to determine half life ✓
links temperature to kinetic energy/speed of particles ✓
energy required to overcome «Coulomb» electrostatic repulsion ✓
«energy is released when» binding energy per nucleon increases
any use of (value from graph) x (number of nucleons) ✓
«235 × 7.6 – (89 × 8.6 + 144 × 8.2) =» 160 «MeV» ✓
Examiners report
The first scientists to identify alpha particles by a direct method were Rutherford and Royds. They knew that radium-226 () decays by alpha emission to form a nuclide known as radon (Rn).
At the start of the experiment, Rutherford and Royds put 6.2 x 10–4 mol of pure radium-226 in a small closed cylinder A. Cylinder A is fixed in the centre of a larger closed cylinder B.
The experiment lasted for 6 days. The decay constant of radium-226 is 1.4 x 10–11 s–1.
At the start of the experiment, all the air was removed from cylinder B. The alpha particles combined with electrons as they moved through the wall of cylinder A to form helium gas in cylinder B.
Write down the nuclear equation for this decay.
Deduce that the activity of the radium-226 is almost constant during the experiment.
Show that about 3 x 1015 alpha particles are emitted by the radium-226 in 6 days.
The wall of cylinder A is made from glass. Outline why this glass wall had to be very thin.
The experiment was carried out at a temperature of 18 °C. The volume of cylinder B was 1.3 x 10–5 m3 and the volume of cylinder A was negligible. Calculate the pressure of the helium gas that was collected in cylinder B over the 6 day period. Helium is a monatomic gas.
Markscheme
OR
These must be seen on the right-hand side of the equation.
ALTERNATIVE 1
6 days is 5.18 x 105 s
activity after 6 days is
OR
A = 0.9999927 A0 or 0.9999927 N0
OR
states that index of e is so small that is ≈ 1
OR
A – A0 ≈ 10–15 «s–1»
ALTERNATIVE 2
shows half-life of the order of 1011 s or 5.0 x 1010 s
converts this to year «1600 y» or days and states half-life much longer than experiment compared to experiment
Award [1 max] if calculations/substitutions have numerical slips but would lead to correct deduction.
eg: failure to convert 6 days to seconds but correct substitution into equation will give MP2.
Allow working in days, but for MP1 must see conversion of or half-life to day–1.
ALTERNATIVE 1
use of A = N0
conversion to number of molecules = nNA = 3.7 x 1020
OR
initial activity = 5.2 x 109 «s–1»
number emitted = (6 x 24 x 3600) x 1.4 x 10–11 x 3.7 x 1020 or 2.7 x 1015 alpha particles
ALTERNATIVE 2
use of N = N0
N0 = n x NA = 3.7 x 1020
alpha particles emitted «= number of atoms disintegrated = N – N0 =» N0 or 2.7 x 1015 alpha particles
Must see correct substitution or answer to 2+ sf for MP3
alpha particles highly ionizing
OR
alpha particles have a low penetration power
OR
thin glass increases probability of alpha crossing glass
OR
decreases probability of alpha striking atom/nucleus/molecule
Do not allow reference to tunnelling.
conversion of temperature to 291 K
p = 4.5 x 10–9 x 8.31 x «»
OR
p = 2.7 x 1015 x 1.3 x 10–23 x «»
0.83 or 0.84 «Pa»
Allow ECF for 2.7 x 1015 from (b)(ii).
Examiners report
Particles can be used in scattering experiments to estimate nuclear sizes.
Electron diffraction experiments indicate that the nuclear radius of carbon-12 is 2.7 x 10–15 m. The graph shows the variation of nuclear radius with nucleon number. The nuclear radius of the carbon-12 is shown on the graph.
The Feynman diagram shows electron capture.
State and explain the nature of the particle labelled X.
Outline how these experiments are carried out.
Outline why the particles must be accelerated to high energies in scattering experiments.
State and explain one example of a scientific analogy.
Plot the position of magnesium-24 on the graph.
Draw a line on the graph, to show the variation of nuclear radius with nucleon number.
Markscheme
«electron» neutrino
it has a lepton number of 1 «as lepton number is conserved»
it has a charge of zero/is neutral «as charge is conserved»
OR
it has a baryon number of 0 «as baryon number is conserved»
Do not allow antineutrino
Do not credit answers referring to energy
«high energy particles incident on» thin sample
detect angle/position of deflected particles
reference to interference/diffraction/minimum/maximum/numbers of particles
Allow “foil” instead of thin
λ OR λ
so high energy gives small λ
to match the small nuclear size
Alternative 2
E = hf/energy is proportional to frequency
frequency is inversely proportional to wavelength/c = fλ
to match the small nuclear size
Alternative 3
higher energy means closer approach to nucleus
to overcome the repulsive force from the nucleus
so greater precision in measurement of the size of the nucleus
Accept inversely proportional
Only allow marks awarded from one alternative
two analogous situations stated
one element of the analogy equated to an element of physics
eg: moving away from Earth is like climbing a hill where the contours correspond to the equipotentials
Atoms in an ideal gas behave like pool balls
The forces between them only act during collisions
correctly plotted
Allow ECF from (d)(i)
single smooth curve passing through both points with decreasing gradient
through origin
Examiners report
During electron capture, an atomic electron is captured by a proton in the nucleus. The stable nuclide thallium-205 () can be formed when an unstable lead (Pb) nuclide captures an electron.
Write down the equation to represent this decay.
The unstable lead nuclide has a half-life of 15 × 106 years. A sample initially contains 2.0 μmol of the lead nuclide. Calculate the number of thallium nuclei being formed each second 30 × 106 years later.
The neutron number N and the proton number Z are not equal for the nuclide . Explain, with reference to the forces acting within the nucleus, the reason for this.
Thallium-205 () can also form from successive alpha (α) and beta-minus (β−) decays of an unstable nuclide. The decays follow the sequence α β− β− α. The diagram shows the position of on a chart of neutron number against proton number.
Draw four arrows to show the sequence of changes to N and Z that occur as the forms from the unstable nuclide.
Markscheme
✓
✓
calculates ✓
calculates nuclei remaining ✓
activity ✓
Accept conversion to seconds at any stage.
Award [3] marks for a bald correct answer.
Allow ECF from MP1 and MP2
Allow use of decay equation.
Reference to proton repulsion OR nucleon attraction ✓
strong force is short range OR electrostatic/electromagnetic force is long range ✓
more neutrons «than protons» needed «to hold nucleus together» ✓
any α change correct ✓
any β change correct ✓
diagram fully correct ✓
Award [2] max for a correct diagram without arrows drawn.
For MP1 accept a (−2, −2 ) line with direction indicated, drawn at any position in the graph.
For MP2 accept a (1, −1) line with direction indicated, drawn at any position in the graph.
Award [1] max for a correct diagram with all arrows in the opposite direction.
Examiners report
The radioactive nuclide beryllium-10 (Be-10) undergoes beta minus (β–) decay to form a stable boron (B) nuclide.
The initial number of nuclei in a pure sample of beryllium-10 is N0. The graph shows how the number of remaining beryllium nuclei in the sample varies with time.
An ice sample is moved to a laboratory for analysis. The temperature of the sample is –20 °C.
Identify the missing information for this decay.
On the graph, sketch how the number of boron nuclei in the sample varies with time.
After 4.3 × 106 years,
Show that the half-life of beryllium-10 is 1.4 × 106 years.
Beryllium-10 is used to investigate ice samples from Antarctica. A sample of ice initially contains 7.6 × 1011 atoms of beryllium-10. The present activity of the sample is 8.0 × 10−3 Bq.
Determine, in years, the age of the sample.
State what is meant by thermal radiation.
Discuss how the frequency of the radiation emitted by a black body can be used to estimate the temperature of the body.
Calculate the peak wavelength in the intensity of the radiation emitted by the ice sample.
The temperature in the laboratory is higher than the temperature of the ice sample. Describe one other energy transfer that occurs between the ice sample and the laboratory.
Markscheme
antineutrino AND charge AND mass number of electron ,
conservation of mass number AND charge ,
Do not accept V.
Accept without subscript e.
[2 marks]
correct shape ie increasing from 0 to about 0.80 N0
crosses given line at 0.50 N0

[2 marks]
ALTERNATIVE 1
fraction of Be = , 12.5%, or 0.125
therefore 3 half lives have elapsed
«≈ 1.4 × 106» «y»
ALTERNATIVE 2
fraction of Be = , 12.5%, or 0.125
leading to λ = 4.836 × 10–7 «y»–1
= 1.43 × 106 «y»
Must see at least one extra sig fig in final answer.
[3 marks]
λ «= » = 4.95 × 10–7 «y–1»
rearranging of A = λN0e–λt to give –λt = ln «= –0.400»
t = «y»
Allow ECF from MP1
[3 marks]
emission of (infrared) electromagnetic/infrared energy/waves/radiation.
[1 mark]
the (peak) wavelength of emitted em waves depends on temperature of emitter/reference to Wein’s Law
so frequency/color depends on temperature
[2 marks]
= 1.1 × 10–5 «m»
Allow ECF from MP1 (incorrect temperature).
[2 marks]
from the laboratory to the sample
conduction – contact between ice and lab surface.
OR
convection – movement of air currents
Must clearly see direction of energy transfer for MP1.
Must see more than just words “conduction” or “convection” for MP2.
[2 marks]
Examiners report
The diagram shows the position of the principal lines in the visible spectrum of atomic hydrogen and some of the corresponding energy levels of the hydrogen atom.
A low-pressure hydrogen discharge lamp contains a small amount of deuterium gas in addition to the hydrogen gas. The deuterium spectrum contains a red line with a wavelength very close to that of the hydrogen red line. The wavelengths for the principal lines in the visible spectra of deuterium and hydrogen are given in the table.
Light from the discharge lamp is normally incident on a diffraction grating.
Determine the energy of a photon of blue light (435nm) emitted in the hydrogen spectrum.
Identify, with an arrow labelled B on the diagram, the transition in the hydrogen spectrum that gives rise to the photon with the energy in (a)(i).
Explain your answer to (a)(ii).
The light illuminates a width of 3.5 mm of the grating. The deuterium and hydrogen red lines can just be resolved in the second-order spectrum of the diffraction grating. Show that the grating spacing of the diffraction grating is about 2 × 10–6 m.
Calculate the angle between the first-order line of the red light in the hydrogen spectrum and the second-order line of the violet light in the hydrogen spectrum.
The light source is changed so that white light is incident on the diffraction grating. Outline the appearance of the diffraction pattern formed with white light.
Markscheme
identifies λ = 435 nm ✔
E = « =» ✔
4.6 ×10−19 «J» ✔
–0.605 OR –0.870 OR –1.36 to –5.44 AND arrow pointing downwards ✔
Arrow MUST match calculation in (a)(i)
Allow ECF from (a)(i)
Difference in energy levels is equal to the energy of the photon ✔
Downward arrow as energy is lost by hydrogen/energy is given out in the photon/the electron falls from a higher energy level to a lower one ✔
«lines» ✔
so spacing is «= 1.9 × 10−6 m» ✔
Allow use of either wavelength or the mean value
Must see at least 2 SF for a bald correct answer
2 × 4.1 × 10−7 = 1.9 × 10−6 sin θv seen
OR
6.6 × 10−7 = 1.9 × 10−6 sin θr seen ✔
θv = 24 − 26 «°»
OR
θr = 19 − 20 «°» ✔
Δθ = 5 − 6 «°» ✔
For MP3 answer must follow from answers in MP2
For MP3 do not allow ECF from incorrect angles
centre of pattern is white ✔
coloured fringes are formed ✔
blue/violet edge of order is closer to centre of pattern
OR
red edge of order is furthest from centre of pattern ✔
the greater the order the wider the pattern ✔
there are gaps between «first and second order» spectra ✔
Examiners report
is formed when a nucleus of deuterium () collides with a nucleus of . The radius of a deuterium nucleus is 1.5 fm.
State how the density of a nucleus varies with the number of nucleons in the nucleus.
Show that the nuclear radius of phosphorus-31 () is about 4 fm.
State the maximum distance between the centres of the nuclei for which the production of is likely to occur.
Determine, in J, the minimum initial kinetic energy that the deuterium nucleus must have in order to produce . Assume that the phosphorus nucleus is stationary throughout the interaction and that only electrostatic forces act.
undergoes beta-minus (β–) decay. Explain why the energy gained by the emitted beta particles in this decay is not the same for every beta particle.
State what is meant by decay constant.
In a fresh pure sample of the activity of the sample is 24 Bq. After one week the activity has become 17 Bq. Calculate, in s–1, the decay constant of .
Markscheme
it is constant ✔
R = «m» ✔
Must see working and answer to at least 2SF
separation for interaction = 5.3 or 5.5 «fm» ✔
energy required = ✔
= 6.5 / 6.6 ×10−13 OR 6.3 ×10−13 «J» ✔
Allow ecf from (b)(i)
«electron» antineutrino also emitted ✔
energy split between electron and «anti»neutrino ✔
probability of decay of a nucleus ✔
OR
the fraction of the number of nuclei that decay
in one/the next second
OR
per unit time ✔
1 week = 6.05 × 105 «s»
17 = ✔
5.7 × 10−7 «s–1» ✔
Award [2 max] if answer is not in seconds
If answer not in seconds and no unit quoted award [1 max] for correct substitution into equation (MP2)
Examiners report
Potassium-40 decays by two processes.
The first process is that of beta-minus (β−) decay to form a calcium (Ca) nuclide.
Potassium-40 decays by a second process to argon-40. This decay accounts for 11 % of the total decay of the potassium-40.
Rocks can be dated by measuring the quantity of argon-40 gas trapped in them. One rock sample contains 340 µmol of potassium-40 and 12 µmol of argon-40.
Write down the equation for this decay.
Show that the initial quantity of potassium-40 in the rock sample was about 450 µmol.
The half-life of potassium-40 is 1.3 × 109 years. Estimate the age of the rock sample.
Outline how the decay constant of potassium-40 was determined in the laboratory for a pure sample of the nuclide.
Markscheme
✓
OR ✓
Full equation
total K-40 decayed = «μmol» ✓
so total K-40 originally was 109 + 340 = 449 «μmol»✓
ALTERNATIVE 1
used to give 𝜆 = 5.3 x 10-10 per year ✓
OR
✓
t = 5.2 x 108 «years» ✓
ALTERNATIVE 2
«remaining» ✓
✓
t = 0.40 x 1.3 x 109 = 5.2 x 108 «years» ✓
ALTERNATIVE 3
«remaining» ✓
✓
t = 0.40 x 1.3 x 109 = 5.2 x 108 «years» ✓
Allow 5.3 x 108 years for final answer.
Allow ECF for MP3 for an incorrect number of half-lives.
«use the mass of the sample to» determine number of potassium-40 atoms / nuclei in sample ✓
«use a counter to» determine (radio)activity / A of sample ✓
use A = λN «to determine the decay constant / λ» ✓
Examiners report
This question was very well done by candidates. The majority were able to identify the correct nuclide of Calcium and many correctly included an electron/beta particle and a properly written antineutrino.
This was a "show that" question that was generally well done by candidates.
This was a more challenging question for candidates. Many were able to calculate the decay constant and recognized that the ratio of initial and final quantities of the potassium-40 was important. A very common error was mixing the two common half-life equations up and using the wrong values in the exponent (using half life instead of the decay constant, or using the decay constant instead of the half life). Examiners were generous with ECF for candidates who clearly showed an incorrect number of half-lives multiplied by the time for one half-life.
Describing methods of determining half-life continues to be a struggle for candidates with very few earning all three marks. Many candidates described a method more appropriate to measuring a short half- life, but even those descriptions fell far short of being acceptable.
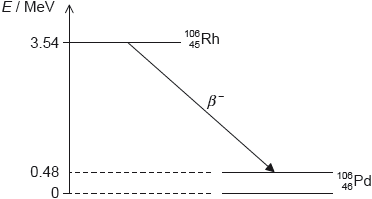
Rhodium-106 () decays into palladium-106 () by beta minus (β–) decay. The diagram shows some of the nuclear energy levels of rhodium-106 and palladium-106. The arrow represents the β– decay.
Bohr modified the Rutherford model by introducing the condition mvr = n. Outline the reason for this modification.
Show that the speed v of an electron in the hydrogen atom is related to the radius r of the orbit by the expression
where k is the Coulomb constant.
Using the answer in (b) and (c)(i), deduce that the radius r of the electron’s orbit in the ground state of hydrogen is given by the following expression.
Calculate the electron’s orbital radius in (c)(ii).
Explain what may be deduced about the energy of the electron in the β– decay.
Suggest why the β– decay is followed by the emission of a gamma ray photon.
Calculate the wavelength of the gamma ray photon in (d)(ii).
Markscheme
the electrons accelerate and so radiate energy
they would therefore spiral into the nucleus/atoms would be unstable
electrons have discrete/only certain energy levels
the only orbits where electrons do not radiate are those that satisfy the Bohr condition «mvr = n»
[3 marks]
OR
KE = PE hence mev2 =
«solving for v to get answer»
Answer given – look for correct working
[1 mark]
combining v = with mevr = using correct substitution
«eg »
correct algebraic manipulation to gain the answer
Answer given – look for correct working
Do not allow a bald statement of the answer for MP2. Some further working eg cancellation of m or r must be shown
[2 marks]
« r = »
r = 5.3 × 10–11 «m»
[1 mark]
the energy released is 3.54 – 0.48 = 3.06 «MeV»
this is shared by the electron and the antineutrino
so the electron’s energy varies from 0 to 3.06 «MeV»
[3 marks]
the palladium nucleus emits the photon when it decays into the ground state «from the excited state»
[1 mark]
Photon energy
E = 0.48 × 106 × 1.6 × 10–19 = «7.68 × 10–14 J»
λ = « =» 2.6 × 10–12 «m»
Award [2] for a bald correct answer
Allow ECF from incorrect energy
[2 marks]