
SL Paper 2
Tomek is attending a conference in Singapore. He has both trousers and shorts to wear. He also has the choice of wearing a tie or not.
The probability Tomek wears trousers is \(0.3\). If he wears trousers, the probability that he wears a tie is \(0.8\).
If Tomek wears shorts, the probability that he wears a tie is \(0.15\).
The following tree diagram shows the probabilities for Tomek’s clothing options at the conference.
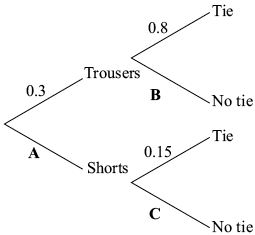
Find the value of
(i) \({\text{A}}\);
(ii) \({\text{B}}\);
(iii) \({\text{C}}\).
Calculate the probability that Tomek wears
(i) shorts and no tie;
(ii) no tie;
(iii) shorts given that he is not wearing a tie.
The conference lasts for two days.
Calculate the probability that Tomek wears trousers on both days.
The conference lasts for two days.
Calculate the probability that Tomek wears trousers on one of the days, and shorts on the other day.
Markscheme
(i) \(0.7 \left( {\frac{{70}}{{100}},{\text{ }}\frac{7}{{10}},{\text{ 70% }}} \right)\) (A1)
(ii) \(0.2 \left( {\frac{{20}}{{100}},{\text{ }}\frac{2}{{10}},{\text{ }}\frac{1}{5},{\text{ 20% }}} \right)\) (A1)
(iii) \(0.85 \left( {\frac{{85}}{{100}},{\text{ }}\frac{{17}}{{20}},{\text{ 85% }}} \right)\) (A1)
[3 marks]
(i) \(0.7 \times 0.85\) (M1)
Note: Award (M1) for multiplying their values from parts (a)(i) and (a)(iii).
\( = 0.595{\text{ }}\left( {\frac{{119}}{{200}},{\text{ 59.5% }}} \right)\) (A1)(ft)(G1)
Note: Follow through from part (a).
(ii) \(0.3 \times 0.2 + 0.7 \times 0.85\) (M1)(M1)
Note: Award (M1) for their two products, (M1) for adding their two products.
\( = 0.655{\text{ }}\left( {\frac{{131}}{{200}},{\text{ 65.5% }}} \right)\) (A1)(ft)(G2)
Note: Follow through from part (a).
(iii) \(\frac{{0.595}}{{0.655}}\) (A1)(ft)(A1)(ft)
Notes: Award (A1)(ft) for correct numerator, (A1)(ft) for correct denominator. Follow through from parts (b)(i) and (ii).
\( = 0.908{\text{ }}\left( {{\text{0.90839}} \ldots ,{\text{ }}\frac{{119}}{{131}},{\text{ 90,8% }}} \right)\) (A1)(ft)(G2)
[8 marks]
\(0.3 \times 0.3\) (M1)
\( = 0.09 \left( {\frac{9}{{100}}, 9\%} \right)\) (A1)(G2)
[2 marks]
\(0.3 \times 0.7\) (M1)
\(0.3 \times 0.7 \times 2\) OR \((0.3 \times 0.7) + (0.7 \times 0.3)\) (M1)
Note: Award (M1) for their correct product seen, (M1) for multiplying their product by 2 or for adding their products twice.
\( = 0.42 \left( {\frac{{42}}{{100}}, \frac{{21}}{{50}}, 42\%} \right)\) (A1)(ft)(G2)
Note: Follow through from part (a)(i).
[3 marks]
Examiners report
A company performs an experiment on the efficiency of a liquid that is used to detect a nut allergy.
A group of 60 people took part in the experiment. In this group 26 are allergic to nuts. One person from the group is chosen at random.
A second person is chosen from the group.
When the liquid is added to a person’s blood sample, it is expected to turn blue if the person is allergic to nuts and to turn red if the person is not allergic to nuts.
The company claims that the probability that the test result is correct is 98% for people who are allergic to nuts and 95% for people who are not allergic to nuts.
It is known that 6 in every 1000 adults are allergic to nuts.
This information can be represented in a tree diagram.
An adult, who was not part of the original group of 60, is chosen at random and tested using this liquid.
The liquid is used in an office to identify employees who might be allergic to nuts. The liquid turned blue for 38 employees.
Find the probability that this person is not allergic to nuts.
Find the probability that both people chosen are not allergic to nuts.
Copy and complete the tree diagram.
Find the probability that this adult is allergic to nuts and the liquid turns blue.
Find the probability that the liquid turns blue.
Find the probability that the tested adult is allergic to nuts given that the liquid turned blue.
Estimate the number of employees, from this 38, who are allergic to nuts.
Markscheme
\(\frac{{34}}{{60}}{\text{ }}\left( {\frac{{17}}{{30}},{\text{ }}0.567,{\text{ }}0.566666 \ldots ,{\text{ }}56.7\% } \right)\) (A1)(A1)
Note: Award (A1) for correct numerator, (A1) for correct denominator.
[2 marks]
\(\frac{{34}}{{60}} \times \frac{{33}}{{59}}\) (M1)
Note: Award (M1) for their correct product.
\( = 0.317{\text{ }}\left( {\frac{{187}}{{590}},{\text{ }}0.316949 \ldots ,{\text{ }}31.7\% } \right)\) (A1)(ft)(G2)
Note: Follow through from part (a).
[2 marks]
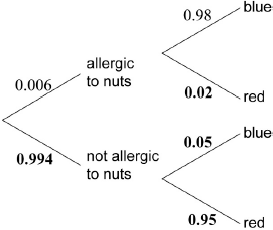 (A1)(A1)(A1)
(A1)(A1)(A1)
Note: Award (A1) for each correct pair of branches.
[3 marks]
\(0.006 \times 0.98\) (M1)
Note: Award (M1) for multiplying 0.006 by 0.98.
\( = 0.00588{\text{ }}\left( {\frac{{147}}{{25000}},{\text{ }}0.588\% } \right)\) (A1)(G2)
[2 marks]
\(0.006 \times 0.98 + 0.994 \times 0.05{\text{ }}(0.00588 + 0.994 \times 0.05)\) (A1)(ft)(M1)
Note: Award (A1)(ft) for their two correct products, (M1) for adding two products.
\( = 0.0556{\text{ }}\left( {0.05558,{\text{ }}5.56\% ,{\text{ }}\frac{{2779}}{{50000}}} \right)\) (A1)(ft)(G3)
Note: Follow through from parts (c) and (d).
[3 marks]
\(\frac{{0.006 \times 0.98}}{{0.05558}}\) (M1)(M1)
Note: Award (M1) for their correct numerator, (M1) for their correct denominator.
\( = 0.106{\text{ }}\left( {0.105793 \ldots ,{\text{ }}10.6\% ,{\text{ }}\frac{{42}}{{397}}} \right)\) (A1)(ft)(G3)
Note: Follow through from parts (d) and (e).
[3 marks]
\(0.105793 \ldots \times 38\) (M1)
Note: Award (M1) for multiplying 38 by their answer to part (f).
\( = 4.02{\text{ }}(4.02015 \ldots )\) (A1)(ft)(G2)
Notes: Follow through from part (f). Use of 3 sf result from part (f) results in an answer of 4.03 (4.028).
[2 marks]
Examiners report
Beartown has three local newspapers: The Art Journal, The Beartown News, and The Currier.
A survey shows that
32 % of the town’s population read The Art Journal,
46 % read The Beartown News,
54 % read The Currier,
3 % read The Art Journal and The Beartown News only,
8 % read The Art Journal and The Currier only,
12 % read The Beartown News and The Currier only, and
5 % of the population reads all three newspapers.
Draw a Venn diagram to represent this information. Label A the set that represents The Art Journal readers, B the set that represents The Beartown News readers, and C the set that represents The Currier readers.
Find the percentage of the population that does not read any of the three newspapers.
Find the percentage of the population that reads exactly one newspaper.
Find the percentage of the population that reads The Art Journal or The Beartown News but not The Currier.
A local radio station states that 83 % of the population reads either The Beartown News or The Currier.
Use your Venn diagram to decide whether the statement is true. Justify your answer.
The population of Beartown is 120 000. The local radio station claimed that 34 000 of the town’s citizens read at least two of the local newspapers.
Find the percentage error in this claim.
Markscheme
(A1) for three circles and a rectangle (U need not be seen)
(A1) for 5
(A1) for 3, 8 and 12
(A1) for 16, 26 and 29 OR 32, 46, 54 placed outside the circles. (A4)
Note: Accept answers given as decimals or fractions.
[4 marks]
100 – (16 + 26 + 29) – (8 + 5 + 3 + 12) (M1)
100 – 71 – 28
Note: Award (M1) for correct expression. Accept equivalent expressions, for example 100 – 71 – 28 or 100 – (71 + 28).
= 1 (A1)(ft)(G2)
Note: Follow through from their Venn diagram but only if working is seen.
[2 marks]
16 + 26 + 29 (M1)
Note: Award (M1) for 16, 26, 29 seen.
= 71 (A1)(ft)(G2)
Note: Follow through from their Venn diagram but only if working is seen.
[2 marks]
16 + 3 + 26 (M1)
Note: Award (M1) for their 16, 3, 26 seen.
= 45 (A1)(ft)(G2)
Note: Follow through from their Venn diagram but only if working is seen.
[2 marks]
True (A1)(ft)
100 – (1 –16) = 83 (R1)(ft)
OR
46 + 54 – 17 = 83 (R1)(ft)
Note: Do not award (A1)(R0). Follow through from their Venn diagram.
[2 marks]
28% of 120000 (M1)
= 33600 (A1)
\({\text{% error}} = \frac{{(34000 - 33600)}}{{33600}} \times 100\) (M1)
Note: Award (M1) for 28 seen (may be implied by 33600 seen), award (M1) for correct substitution of their 33600 in the percentage error formula. If an error is made in calculating 33600 award a maximum of (M1)(A0)(M1)(A0), the final accuracy mark is lost.
OR
\(\frac{{34000}}{{120000}} \times 100\) (M1)
= 28.3(28.3333…) (A1)
\({\text{% error}} = \frac{{(28.3333... - 28)}}{{28}} \times 100\) (M1)
= 1.19% (1.19047...) (A1)(ft)(G3)
Note: % sign not required. Accept 1.07 (1.0714…) with use of 28.3. 1.18 with use of 28.33 and 1.19 with use of 28.333. Award (G3) for 1.07, 1.18 or 1.19 seen without working.
[4 marks]
Examiners report
This question was accessible to the great majority of candidates. The common errors were:
- the lack of a bounding rectangle in (a);
- the lack of subtraction for the entries in the disjoint regions of the type \(A' \cap B' \cap C\) and the subsequent total exceeding 100%;
- the incorrect interpretation of “either ...or” as “exclusive or”. It is of the utmost importance to note that the ambiguity of the “or” statement will be removed and “exclusive or” signalled by the phrase “either ...or....but not both”. Otherwise, “inclusive or” must always be assumed.
A number of candidates were unable to interpret the percentage error question correctly and scored 0/4. This was somewhat disappointing.
This question was accessible to the great majority of candidates. The common errors were:
- the lack of a bounding rectangle in (a);
- the lack of subtraction for the entries in the disjoint regions of the type \(A' \cap B' \cap C\) and the subsequent total exceeding 100%;
- the incorrect interpretation of “either ...or” as “exclusive or”. It is of the utmost importance to note that the ambiguity of the “or” statement will be removed and “exclusive or” signalled by the phrase “either ...or....but not both”. Otherwise, “inclusive or” must always be assumed.
A number of candidates were unable to interpret the percentage error question correctly and scored 0/4. This was somewhat disappointing.
This question was accessible to the great majority of candidates. The common errors were:
- the lack of a bounding rectangle in (a);
- the lack of subtraction for the entries in the disjoint regions of the type \(A' \cap B' \cap C\) and the subsequent total exceeding 100%;
- the incorrect interpretation of “either ...or” as “exclusive or”. It is of the utmost importance to note that the ambiguity of the “or” statement will be removed and“exclusive or” signalled by the phrase “either ...or....but not both”. Otherwise, “inclusive or” must always be assumed.
A number of candidates were unable to interpret the percentage error question correctly and scored 0/4. This was somewhat disappointing.
This question was accessible to the great majority of candidates. The common errors were:
- the lack of a bounding rectangle in (a);
- the lack of subtraction for the entries in the disjoint regions of the type \(A' \cap B' \cap C\) and the subsequent total exceeding 100%;
- the incorrect interpretation of “either ...or” as “exclusive or”. It is of the utmost importance to note that the ambiguity of the “or” statement will be removed and “exclusive or” signalled by the phrase “either ...or....but not both”. Otherwise, “inclusive or” must always be assumed.
A number of candidates were unable to interpret the percentage error question correctly and scored 0/4. This was somewhat disappointing.
This question was accessible to the great majority of candidates. The common errors were:
- the lack of a bounding rectangle in (a);
- the lack of subtraction for the entries in the disjoint regions of the type \(A' \cap B' \cap C\) and the subsequent total exceeding 100%;
- the incorrect interpretation of “either ...or” as “exclusive or”. It is of the utmost importance to note that the ambiguity of the “or” statement will be removed and “exclusive or” signalled by the phrase “either ...or....but not both”. Otherwise, “inclusive or” must always be assumed.
A number of candidates were unable to interpret the percentage error question correctly and scored 0/4. This was somewhat disappointing.
This question was accessible to the great majority of candidates. The common errors were:
- the lack of a bounding rectangle in (a);
- the lack of subtraction for the entries in the disjoint regions of the type \(A' \cap B' \cap C\) and the subsequent total exceeding 100%;
- the incorrect interpretation of “either ...or” as “exclusive or”. It is of the utmost importance to note that the ambiguity of the “or” statement will be removed and“exclusive or” signalled by the phrase “either ...or....but not both”. Otherwise, “inclusive or” must always be assumed.
A number of candidates were unable to interpret the percentage error question correctly and scored 0/4. This was somewhat disappointing.
A survey of 100 families was carried out, asking about the pets they own. The results are given below.
56 owned dogs (S)
38 owned cats (Q)
22 owned birds (R)
16 owned dogs and cats, but not birds
8 owned birds and cats, but not dogs
3 owned dogs and birds, but not cats
4 owned all three types of pets
Draw a Venn diagram to represent this information.
Find the number of families who own no pets.
Find the percentage of families that own exactly one pet.
A family is chosen at random. Find the probability that they own a cat, given that they own a bird.
Markscheme
(A1)(A1)(A1)(A1)(A1)
Note: Award (A1) for rectangle (U not required), (A1) for 3 intersecting circles, (A1) for 4 in central intersection, (A1) for 16, 3, 8 and (A1) for 33, 10, 7 (ft) if subtraction is carried out, or for S(56), Q(38) and R(22) seen by the circles.
[5 marks]
100 − 81 (M1)
19 (A1)(ft)(G2)
Note: Award (M1) for subtracting their total from 100.
[2 marks]
\(33 +10 + 7\) (M1)
Note: Award (M1) for adding their values from (a).
\(\left( {\frac{{50}}{{100}}} \right) \times 100{\text{ }}\% \) (A1)(ft)
50 % (50) (A1)(ft)(G3)
[3 marks]
P (own a cat given they own a bird) \( = \frac{{12}}{{22}}\left( {0.545,\frac{6}{{11}}} \right)\) (A1)(ft)(A1)(ft)
Note: Award (A1)(ft) for the numerator, (A1)(ft) for the denominator.
[2 marks]
Examiners report
Most candidates began the paper well by correctly drawing the Venn diagram and answering parts (b) and (c) correctly.
Most candidates began the paper well by correctly drawing the Venn diagram and answering parts (b) and (c) correctly.
Most candidates began the paper well by correctly drawing the Venn diagram and answering parts (b) and (c) correctly.
Conditional probability has proved difficult for many candidates; only a very small part of the candidates scored full marks for this part.
Pam has collected data from a group of 400 IB Diploma students about the Mathematics course they studied and the language in which they were examined (English, Spanish or French). The summary of her data is given below.
A student is chosen at random from the group. Find the probability that the student
(i) studied Mathematics HL;
(ii) was examined in French;
(iii) studied Mathematics HL and was examined in French;
(iv) did not study Mathematics SL and was not examined in English;
(v) studied Mathematical Studies SL given that the student was examined in Spanish.
Pam believes that the Mathematics course a student chooses is independent of the language in which the student is examined.
Using your answers to parts (a) (i), (ii) and (iii) above, state whether there is any evidence for Pam’s belief. Give a reason for your answer.
Pam decides to test her belief using a Chi-squared test at the \(5\% \) level of significance.
(i) State the null hypothesis for this test.
(ii) Show that the expected number of Mathematical Studies SL students who took the examination in Spanish is \(41.3\), correct to 3 significant figures.
Write down
(i) the Chi-squared calculated value;
(ii) the number of degrees of freedom;
(iii) the Chi-squared critical value.
State, giving a reason, whether there is sufficient evidence at the \(5\% \) level of significance that Pam’s belief is correct.
Markscheme
(i) \(\frac{{100}}{{400}}{\text{ }}\left( {\frac{1}{4}{\text{, }}0.25{\text{, }}25\% } \right)\) (A1)
(ii) \(\frac{{90}}{{400}}{\text{ }}\left( {\frac{9}{{40}}{\text{, }}0.225{\text{, }}22.5\% } \right)\) (A1)
(iii) \(\frac{{20}}{{400}}{\text{ }}\left( {\frac{1}{{20}}{\text{, }}0.05{\text{, }}5\% } \right)\) (A1)(A1)
Note: Award (A1) for numerator, (A1) for denominator.
(iv) \(\frac{{120}}{{400}}{\text{ }}\left( {\frac{3}{{10}}{\text{, }}0.3{\text{, }}30\% } \right)\) (A1)(A1)
Note: Award (A1) for numerator, (A1) for denominator.
(v) \(\frac{{30}}{{110}}{\text{ }}\left( {\frac{3}{{11}}{\text{, }}0.273{\text{, }}27.3\% } \right)\) (\(0.272727 \ldots \)) (A1)(A1)
Note: Award (A1) for numerator, (A1) for denominator. Accept \(0.27\), do not accept \(0.272\), do not accept \(0.3\).
[8 marks]
\(\frac{1}{{20}} \ne \frac{1}{4} \times \frac{9}{{40}}\) (R1)(ft)
Note: The fractions must be used as part of the reason. Follow through from (a)(i), (a)(ii) and (a)(iii).
Pam is not correct. (A1)(ft)
Notes: Do not award (R0)(A1). Accept the events are not independent (dependent).
[2 marks]
(i) The mathematics course and language of examination are independent. (A1)
Notes: Accept “There is no association between Mathematics course and language”. Do not accept “not related”, “not correlated”, “not influenced”.
(ii) \(\frac{{110}}{{400}} \times \frac{{150}}{{400}} \times 400{\text{ }}\left( { = \frac{{110 \times 150}}{{400}}} \right)\) (M1)
\( = 41.25\) (A1)
\( = 41.3\) (AG)
Note: \(41.25\) and \(41.3\) must be seen to award final (A1).
[3 marks]
(i) \(7.67\) (\(7.67003 \ldots \)) (G2)
Note: Accept \(7.7\), do not accept \(8\) or \(7.6\). Award (G1) if formula with all nine terms seen but their answer is not one of those above.
(ii) \(4\) (G1)
(iii) \(9.488\) (A1)(ft)
Notes: Accept \(9.49\) or \(9.5\), do not accept \(9.4\) or \(9\). Follow through from their degrees of freedom.
[4 marks]
\(7.67 < 9.488\) (R1)
OR
\(p = 0.104 \ldots , p > 0.05\) (R1)
Accept (Do not reject) \({H_0}\) (Pam’s belief is correct) (A1)(ft)
Notes: Follow through from part (d). Do not award (R0)(A1).
[2 marks]
Examiners report
The simple probabilities beginning this question were successfully attempted by the great majority. Most errors in the latter parts occurred due to candidates trying to use the algebraic form of laws of probability, rather than by interpreting the contingency table. Probability questions in this course are, in the main, contextual and the reliance of formulas is not always beneficial to the candidates. Only the best candidates realized the significance of part (b) as a link to the chi-squared test.
This was well attempted by the majority, the weakness being the sole reliance of the calculator to calculate expected value. However, there still remains confusion between critical and p-values as the basis for accepting the null hypothesis.
The simple probabilities beginning this question were successfully attempted by the great majority. Most errors in the latter parts occurred due to candidates trying to use the algebraic form of laws of probability, rather than by interpreting the contingency table. Probability questions in this course are, in the main, contextual and the reliance of formulas is not always beneficial to the candidates. Only the best candidates realized the significance of part (b) as a link to the chi-squared test.
This was well attempted by the majority, the weakness being the sole reliance of the calculator to calculate expected value. However, there still remains confusion between critical and \(p\)-values as the basis for accepting the null hypothesis.
The simple probabilities beginning this question were successfully attempted by the great majority. Most errors in the latter parts occurred due to candidates trying to use the algebraic form of laws of probability, rather than by interpreting the contingency table. Probability questions in this course are, in the main, contextual and the reliance of formulas is not always beneficial to the candidates. Only the best candidates realized the significance of part (b) as a link to the chi-squared test.
This was well attempted by the majority, the weakness being the sole reliance of the calculator to calculate expected value. However, there still remains confusion between critical and \(p\)-values as the basis for accepting the null hypothesis.
The simple probabilities beginning this question were successfully attempted by the great majority. Most errors in the latter parts occurred due to candidates trying to use the algebraic form of laws of probability, rather than by interpreting the contingency table. Probability questions in this course are, in the main, contextual and the reliance of formulas is not always beneficial to the candidates. Only the best candidates realized the significance of part (b) as a link to the chi-squared test.
This was well attempted by the majority, the weakness being the sole reliance of the calculator to calculate expected value. However, there still remains confusion between critical and \(p\)-values as the basis for accepting the null hypothesis.
The simple probabilities beginning this question were successfully attempted by the great majority. Most errors in the latter parts occurred due to candidates trying to use the algebraic form of laws of probability, rather than by interpreting the contingency table. Probability questions in this course are, in the main, contextual and the reliance of formulas is not always beneficial to the candidates. Only the best candidates realized the significance of part (b) as a link to the chi-squared test.
This was well attempted by the majority, the weakness being the sole reliance of the calculator to calculate expected value. However, there still remains confusion between critical and \(p\)-values as the basis for accepting the null hypothesis.
Leanne goes fishing at her favourite pond. The pond contains four different types of fish: bream, flathead, whiting and salmon. The fish are either undersized or normal. This information is shown in the table below.
Write down the total number of fish in the pond.
Leanne catches a fish.
Find the probability that she
(i) catches an undersized bream;
(ii) catches either a flathead or an undersized fish or both;
(iii) does not catch an undersized whiting;
(iv) catches a whiting given that the fish was normal.
Leanne notices that on windy days, the probability she catches a fish is 0.1 while on non-windy days the probability she catches a fish is 0.65. The probability that it will be windy on a particular day is 0.3.
Copy and complete the probability tree diagram below.
Leanne notices that on windy days, the probability she catches a fish is 0.1 while on non-windy days the probability she catches a fish is 0.65. The probability that it will be windy on a particular day is 0.3.
Calculate the probability that it is windy and Leanne catches a fish on a particular day.
Leanne notices that on windy days, the probability she catches a fish is 0.1 while on non-windy days the probability she catches a fish is 0.65. The probability that it will be windy on a particular day is 0.3.
Calculate the probability that Leanne catches a fish on a particular day.
Use your answer to part (e) to calculate the probability that Leanne catches a fish on two consecutive days.
Leanne notices that on windy days, the probability she catches a fish is 0.1 while on non-windy days the probability she catches a fish is 0.65. The probability that it will be windy on a particular day is 0.3.
Given that Leanne catches a fish on a particular day, calculate the probability that the day was windy.
Markscheme
90 (A1)
[1 mark]
(i) \(\frac{3}{{90}}(0.0\bar 3,{\text{ }}0.0333,{\text{ }}0.0333...,{\text{ }}3.\bar 3\% ,{\text{ }}3.33\% )\) (A1)(ft)
Note: For the denominator follow through from their answer in part (a).
(ii) \(\frac{{53}}{{90}}(0.5\bar 8,{\text{ }}0.588...,{\text{ }}0.589,{\text{ }}58.\bar 8\% ,{\text{ }}58.9\% )\) (A1)(A1)(ft)(G2)
Notes: Award (A1) for the numerator. (A1)(ft) for denominator. For the denominator follow through from their answer in part (a).
(iii) \(\frac{{72}}{{90}}{\text{(0.8, 80}}\%)\) (A1)(ft)(A1)(ft)(G2)
Notes: Award (A1)(ft) for the numerator, (their part (a) –18) (A1)(ft) for denominator. For the denominator follow through from their answer in part (a).
(iv) \(\frac{{24}}{{48}}(0.5,{\text{ 50}}\% )\) (A1)(A1)(G2)
Note: Award (A1) for numerator, (A1) for denominator.
[7 marks]
(A1)(A1)(A1)
Notes: Award (A1) for each correct entry. Tree diagram must be seen for marks to be awarded.
[3 marks]
\(0.3 \times 0.1 = 0.03\left( {\frac{3}{{100}}} \right)\) (M1)(A1)(G2)
Note: Award (M1) for correct product seen.
[2 marks]
\(0.3 \times 0.1+ 0.7\times0.65\) (M1)(M1)
Notes: Award (M1) for \(0.7\times0.65\) (or 0.455) seen, (M1) for adding their 0.03. Follow through from their answers to parts (c) and (d).
\( = 0.485\left( {\frac{{485}}{{1000}},\frac{{97}}{{200}}} \right)\) (A1)(ft)(G2)
Note: Follow through from their tree diagram and their answer to part (d).
[3 marks]
\(0.485 \times 0.485\) (M1)
\(0.235\left( {\frac{{9409}}{{40000}}{\text{, }}0.235225} \right)\) (A1)(ft)(G2)
Note: Follow through from their answer to part (e).
[2 marks]
\(\frac{{0.03}}{{0.485}}\) (M1)(A1)(ft)
Notes: Award (M1) for substituted conditional probability formula, (A1)(ft) for their (d) as numerator and their (e) as denominator.
\(0.0619\left( {\frac{{6}}{{97}}}\text{, 0.0618556...} \right) \) (A1)(ft)(G2)
Note: Follow through from their parts (d) and (e).
[3 marks]
Examiners report
(a) Most candidates found this correctly although a few wrote 180 instead of 90.
(b) This was also answered well. The main errors were putting 65/90 in part (ii) and 24/90 in part (iv).
(c) The tree diagram was completed correctly in most scripts. It appears that some candidates may have answered this on their question paper and this was not sent to the scanning centre with the answer papers.
(d) Many answered this correctly. Some added instead of multiplying.
(e) Surprisingly well answered. Again some added and multiplied in the wrong place.
(f) Most candidates added here and then divided by 2 rather than multiplying.
(g) This was badly done with very few correct answers seen.
A geometric sequence has second term 12 and fifth term 324.
Consider the following propositions
p: The number is a multiple of five.
q: The number is even.
r: The number ends in zero.
Calculate the value of the common ratio.
Calculate the 10th term of this sequence.
The kth term is the first term which is greater than 2000. Find the value of k.
Write in words \((q \wedge \neg r) \Rightarrow \neg p\).
Consider the statement “If the number is a multiple of five, and is not even then it will not end in zero”.
Write this statement in symbolic form.
Consider the statement “If the number is a multiple of five, and is not even then it will not end in zero”.
Write the contrapositive of this statement in symbolic form.
Markscheme
u1r4 = 324 (A1)
u1r = 12 (A1)
r3 = 27 (M1)
r = 3 (A1)(G3)
Note: Award at most (G3) for trial and error.
[4 marks]
4 × 39 = 78732 or 12 × 38 = 78732 (A1)(M1)(A1)(ft)(G3)
Note: Award (A1) for u1 = 4 if n = 9 , or u1 = 12 if n = 8, (M1) for correctly substituted formula.
(ft) from their (a).
[3 marks]
4 × 3k−1 > 2000 (M1)
Note: Award (M1) for correct substitution in correct formula. Accept an equation.
k > 6 (A1)
k = 7 (A1)(ft)(G2)
Notes: If second line not seen award (A2) for correct answer. (ft) from their (a).
Accept a list, must see at least 3 terms including the 6th and 7th.
Note: If arithmetic sequence formula is used consistently in parts (a), (b) and (c), award (A0)(A0)(M0)(A0) for (a) and (ft) for parts (b) and (c).
[3 marks]
If the number is even and the number does not end in zero, (then) the number is not a multiple of five. (A1)(A1)(A1)
Note: Award (A1) for “if…(then)”, (A1) for “the number is even and the number does not end in zero”, (A1) for the number is not a multiple of 5.
[3 marks]
\((p \wedge \neg q) \Rightarrow \neg r\) (A1)(A1)(A1)(A1)
(A1) for \(\Rightarrow\), (A1) for \(\wedge\), (A1) for p and \(\neg q\), (A1) for \(\neg r\)
Note: If parentheses not present award at most (A1)(A1)(A1)(A0).
[4 marks]
\(r \Rightarrow (\neg p \vee q)\) OR \(r \Rightarrow \neg (p \wedge \neg q)\) (A1)(ft)(A1)(ft)
Note: Award (A1)(ft) for reversing the order, (A1) for negating the statements on both sides.
If parentheses not present award at most (A1)(ft)(A0).
Do not penalise twice for missing parentheses in (i) and (ii).
[2 marks]
Examiners report
An easy ratio to find and the majority of candidates found r = 3, though many had trouble showing the appropriate method, thus losing marks.
A fairly straightforward part for most candidates.
The majority found k − 7; many without supporting work which lost them a mark. Where candidates had difficulty in this part, it was generally a case of poor algebraic skills.
This question on logic was straightforward for most candidates who scored full marks for parts (a) and (b) (i). A few omitted the brackets in part (b).
This question on logic was straightforward for most candidates who scored full marks for parts (a) and (b) (i). A few omitted the brackets in part (b).
Very poorly answered with many candidates scoring just one mark. The main error was to open the bracket and not use the “or”.
In a company it is found that 25 % of the employees encountered traffic on their way to work. From those who encountered traffic the probability of being late for work is 80 %.
From those who did not encounter traffic, the probability of being late for work is 15 %.
The tree diagram illustrates the information.
The company investigates the different means of transport used by their employees in the past year to travel to work. It was found that the three most common means of transport used to travel to work were public transportation (P ), car (C ) and bicycle (B ).
The company finds that 20 employees travelled by car, 28 travelled by bicycle and 19 travelled by public transportation in the last year.
Some of the information is shown in the Venn diagram.
There are 54 employees in the company.
Write down the value of a.
Write down the value of b.
Use the tree diagram to find the probability that an employee encountered traffic and was late for work.
Use the tree diagram to find the probability that an employee was late for work.
Use the tree diagram to find the probability that an employee encountered traffic given that they were late for work.
Find the value of x.
Find the value of y.
Find the number of employees who, in the last year, did not travel to work by car, bicycle or public transportation.
Find \(n\left( {\left( {C \cup B} \right) \cap P'} \right)\).
Markscheme
a = 0.2 (A1)
[1 mark]
b = 0.85 (A1)
[1 mark]
0.25 × 0.8 (M1)
Note: Award (M1) for a correct product.
\( = 0.2\,\,\,\left( {\,\frac{1}{5},\,\,\,20\% } \right)\) (A1)(G2)
[2 marks]
0.25 × 0.8 + 0.75 × 0.15 (A1)(ft)(M1)
Note: Award (A1)(ft) for their (0.25 × 0.8) and (0.75 × 0.15), (M1) for adding two products.
\( = 0.313\,\,\,\left( {0.3125,\,\,\,\frac{5}{{16}},\,\,\,31.3\% } \right)\) (A1)(ft)(G3)
Note: Award the final (A1)(ft) only if answer does not exceed 1. Follow through from part (b)(i).
[3 marks]
\(\frac{{0.25 \times 0.8}}{{0.25 \times 0.8 + 0.75 \times 0.15}}\) (A1)(ft)(A1)(ft)
Note: Award (A1)(ft) for a correct numerator (their part (b)(i)), (A1)(ft) for a correct denominator (their part (b)(ii)). Follow through from parts (b)(i) and (b)(ii).
\( = 0.64\,\,\,\left( {\frac{{16}}{{25}},\,\,64{\text{% }}} \right)\) (A1)(ft)(G3)
Note: Award final (A1)(ft) only if answer does not exceed 1.
[3 marks]
(x =) 3 (A1)
[1 Mark]
(y =) 10 (A1)(ft)
Note: Following through from part (c)(i) but only if their x is less than or equal to 13.
[1 Mark]
54 − (10 + 3 + 4 + 2 + 6 + 8 + 13) (M1)
Note: Award (M1) for subtracting their correct sum from 54. Follow through from their part (c).
= 8 (A1)(ft)(G2)
Note: Award (A1)(ft) only if their sum does not exceed 54. Follow through from their part (c).
[2 marks]
6 + 8 + 13 (M1)
Note: Award (M1) for summing 6, 8 and 13.
27 (A1)(G2)
[2 marks]
Examiners report
Consider these three propositions, in which x is a natural number.
\[\begin{array}{*{20}{l}} {p{\text{: }}x{\text{ is a factor of 60}}} \\ {q{\text{: }}x{\text{ is a multiple of 4}}} \\ {r{\text{: }}x{\text{ is a multiple of 5}}} \end{array}\]
Write down in symbolic form the compound proposition
“If \(x\) is a factor of 60 then \(x\) is a multiple of 5 or \(x\) is not a multiple of 4.”
Write down in words the compound proposition \(\neg r \wedge (p\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{ \vee } q)\).
Copy the following truth table and complete the last three columns.
State why the compound proposition \(\neg r \wedge (p\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{ \vee } q)\) is not a logical contradiction.
A row from the truth table from part (c) is given below.

Write down one value of \(x\) that satisfies these truth values.
Markscheme
\(p \Rightarrow (r \vee \neg q)\) (A1)(A1)(A1)
Note: Award (A1) for “\(p \Rightarrow \)”.
Award (A1) for “\(r \vee \neg q\)” or “\(r \vee q\)” (or “\(\neg q \vee r\)”or “\(q \vee r\)”)
Award (A1) for “\(\neg q\)”.
Award at most (A1)(A1)(A0) if parentheses are missing for \(r \vee \neg q\).
Award (A0)(A0)(A1) for \((p \Rightarrow r) \vee \neg q\).
[3 marks]
\(x\) is not a multiple of 5 and (\(x\)) is (either) a factor of 60 or (\(x\)) is a multiple of 4, but not both (A1)(A1)(A1)
Note: Award (A1) for “\(x\) is not a multiple of 5”, (A1) for “(\(x\)) is a factor of 60 or (\(x\)) is a multiple of 4 but not both”, (A1) for “and” in the correct position. Accept only “but not both” in the second (A1).
Award at most (A1)(A1)(A0) for using extra statements such as “If ...then”, “if and only if” etc.
[3 marks]
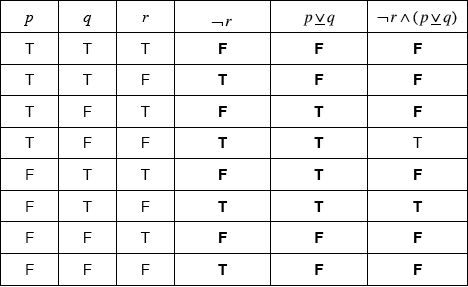 (A1)(A1)(A1)(ft)
(A1)(A1)(A1)(ft)
Note: Award (A1) for each correct column. Last column follows through from previous two.
[3 marks]
because not all the entries in the \(\neg r \wedge (p\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{ \vee } q)\) column are F (R1)(ft)
Note: If all entries in the last column of their truth table are T, award (R1)(ft) for an answer of “it is a tautology”. Only award (R1)(ft) if the column is identified in the justification.
[1 mark]
accept one of: 1\(\,\,\,\)OR\(\,\,\,\)2\(\,\,\,\)OR\(\,\,\,\)3\(\,\,\,\)OR\(\,\,\,\)6 (A1)
Note: Award (A1) for any one of the above answers.
[1 mark]
Examiners report
Forty families were surveyed about the places they went to on the weekend. The places were the circus (C), the museum (M) and the park (P).
16 families went to the circus
22 families went to the museum
14 families went to the park
4 families went to all three places
7 families went to both the circus and the museum, but not the park
3 families went to both the circus and the park, but not the museum
1 family went to the park only
Draw a Venn diagram to represent the given information using sets labelled C, M and P. Complete the diagram to include the number of families represented in each region.
Find the number of families who
(i) went to the circus only;
(ii) went to the museum and the park but not the circus;
(iii) did not go to any of the three places on the weekend.
A family is chosen at random from the group of 40 families. Find the probability that the family went to
(i) the circus;
(ii) two or more places;
(iii) the park or the circus, but not the museum;
(iv) the museum, given that they also went to the circus.
Two families are chosen at random from the group of 40 families.
Find the probability that both families went to the circus.
Markscheme
(A1)(A1)(A1)(A1)
Award (A1) for 3 intersecting circles and rectangle, (A1) for 1, 3, 4 and 7, (A1) for 2, (A1) for 6 and 5.
(i) 2 (A1)(ft)
(ii) 6 (A1)(ft)
(iii) 40 − (1 + 6 + 2 + 3 + 4 + 7 + 5) (M1)
Note: Award (M1) for subtracting all their values from 40.
= 12 (A1)(ft)(G2)
Note: Follow through from their Venn diagram for parts (i), (ii) and (iii).
(i) \(\frac{{16}}{{40}}\left( {\frac{2}{5},0.4,40\% } \right)\) (A1)(A1)(G2)
Note: Award (A1) for numerator, (A1) for denominator. Answer must be less than 1 otherwise award (A0)(A0). Award (A0)(A0) if answer is given as incorrect reduced fraction without working.
(ii) \(\frac{{20}}{{40}}\left( {\frac{1}{2},0.5,50\% } \right)\) (A1)(ft) (A1) (G2)
Note: Award (A1)(ft) for numerator, (A1) for denominator. Follow through from their Venn diagram. Answer must be less than 1 otherwise award (A0)(A0). Award (A0)(A0) if answer is given as incorrect reduced fraction without working.
(iii) \(\frac{6}{{40}}\left( {\frac{3}{{20}},0.15,15\% } \right)\) (A1)(ft)(A1)(G2)
Note: Award (A1)(ft) for numerator, (A1) for denominator. Follow through from their Venn diagram. Answer must be less than 1 otherwise award (A0)(A0). Award (A0)(A0) if answer is given as incorrect reduced fraction without working.
(iv) \(\frac{{11}}{{16}}\left( {0.6875,68.75\% } \right)\) (A1)(ft)(A1)(G2)
Note: Award (A1)(ft) for numerator, (A1) for denominator. Follow through from their Venn diagram. Answer must be less than 1 otherwise award (A0)(A0). Award (A0)(A0) if answer is given as incorrect reduced fraction without working.
\(\frac{{16}}{{40}} \times \frac{{15}}{{39}}\) (A1)(A1)(ft)
Note: Award (A1) for multiplication of their probabilities, (A1)(ft) for their correct probabilities.
\(\frac{{240}}{{1560}}\left( {\frac{2}{{13}},0.153846...,15.4\% } \right)\) (A1)(ft)(G2)
Note: Follow through from their answer to part (c)(i). Answer must be less than 1 otherwise award at most (A1)(A1)(A0)(ft).
Examiners report
A group of tourists went on safari to a game reserve. The game warden wanted to know how many of the tourists saw Leopard (\(L\)), Cheetah (\(C\)) or Rhino (\(R\)). The results are given as follows.
5 of the tourists saw all three
7 saw Leopard and Rhino
1 saw Cheetah and Leopard but not Rhino
4 saw Leopard only
3 saw Cheetah only
9 saw Rhino only
Draw a Venn diagram to show this information.
There were 25 tourists in the group and every tourist saw at least one of the three types of animal.
Find the number of tourists that saw Cheetah and Rhino but not Leopard.
There were 25 tourists in the group and every tourist saw at least one of the three types of animal.
Calculate the probability that a tourist chosen at random from the group
(i) saw Leopard;
(ii) saw only one of the three types of animal;
(iii) saw only Leopard, given that he saw only one of the three types of animal.
There were 25 tourists in the group and every tourist saw at least one of the three types of animal.
If a tourist chosen at random from the group saw Leopard, find the probability that he also saw Cheetah.
Markscheme
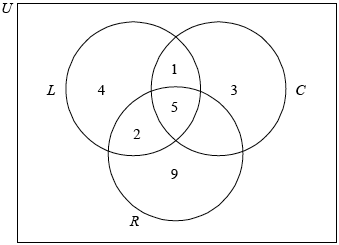 (A1)(A1)(A1)(A1)
(A1)(A1)(A1)(A1)
Note: Award (A1) for rectangle and three labelled intersecting circles (the rectangle need not be labelled), (A1) for 5, (A1) for 2 and 1, (A1) for 4, 3 and 9.
[4 marks]
\(25 - (5 + 2 + 1 + 4 + 3 + 9)\) (M1)
Notes: Award (M1) for their \(5 + 2 + 1 + 4 + 3 + 9\) seen even if total is greater than \(25\).
Do not award (A1)(ft) if their total is greater than \(25\).
\( = 1\) (A1)(ft)(G2)
[2 marks]
(i) \(\frac{{12}}{{25}}{\text{ }}(0.48,{\text{ }}48\% )\) (A1)(ft)(A1)(G2)
Notes: Award (A1)(ft) for numerator, (A1) for denominator.
Follow through from Venn diagram.
(ii) \(\frac{{16}}{{25}}{\text{ }}(0.64,{\text{ }}64\% )\) (A1)(A1)(G2)
Notes: Award (A1) for numerator, (A1) for denominator.
There is no follow through; all information is given.
(iii) \(\frac{4}{{16}}{\text{ }}(0.25,{\text{ }}25\% )\)) (A1)(A1)(ft)(G2)
Notes: Award (A1) for numerator, (A1)(ft) for denominator.
Follow through from part (c)(ii) only.
[6 marks]
\(\frac{6}{{12}}{\text{ }}(0.5,{\text{ }}50\% )\) (A1)(A1)(ft)(G2)
Notes: Award (A1) for numerator, (A1)(ft) for denominator.
Follow through from Venn diagram.
[2 marks]
Examiners report
Consider the following statements.
\(p\): the land has been purchased
\(q\): the building permit has been obtained
\(r\): the land can be used for residential purposes
Write the following argument in symbolic form.
“If the land has been purchased and the building permit has been obtained, then the land can be used for residential purposes.”
In your answer booklet, copy and complete a truth table for the argument in part (a).
Begin your truth table as follows.
Use your truth table to determine whether the argument in part (a) is valid.
Give a reason for your decision.
Write down the inverse of the argument in part (a)
(i) in symbolic form;
(ii) in words.
Markscheme
\((p \wedge q) \Rightarrow r\) (A1)(A1)(A1)
Notes: Award (A1) for conjunction seen, award (A1) for implication seen, award (A1) for correct simple propositions in correct order (the parentheses are required). Accept \(r \Leftarrow (p \wedge q)\).
 (A1)(ft)(A1)(ft)
(A1)(ft)(A1)(ft)
Notes: Award (A1)(ft) for each correct column, follow through to the final column from their \((p \wedge q)\) column. For the second (A1)(ft) to be awarded there must be an implication in part (a).
Follow through from part (a).
The argument is not valid since not all entries in the final column are T. (A1)(ft)(R1)
Notes: Do not award (A1)(ft)(R0). Follow through from part (b).
Accept “The argument is not valid since \((p \wedge q) \Rightarrow r\) is not a tautology”.
(i) \(\neg (p \wedge q) \Rightarrow \neg r\) (A1)(ft)(A1)(ft)
OR
\((\neg p \vee \neg q) \Rightarrow \neg r\) (A1)(ft)(A1)(ft)
Notes: Award (A1)(ft) for the negation of their antecedent and the negation of their consequent, (A1)(ft) for their fully correct answer.
Follow through from part (a). Accept \(\neg r \Leftarrow \neg (p \wedge q)\) or \(\neg r \Leftarrow (\neg p \vee \neg q)\). Follow through from part (a).
(ii) if it is not the case that the land has been purchased and the building permit has been obtained then the land can not be used for residential purposes. (A1)(A1)(ft)
OR
if (either) the land has not been purchased or the building permit has not been obtained then the land can not be used for residential purposes. (A1)(A1)(ft)
Notes: Award (A1) for “if… then…” seen, (A1)(ft) for correct statements in correct order. Follow through from part (d)(i).
Examiners report
Forming the statement in part (a) was attainable by the great majority, although the lack of parentheses was a common fault.
The truth table in part (b) saw less success and it was clear that some centres simply had not prepared their candidates in this area of the course.
Where the truth table was correctly constructed many candidates were not aware of the conditions required for an argument to be valid and in part (d) the converse and the inverse were often confused.
Where the truth table was correctly constructed many candidates were not aware of the conditions required for an argument to be valid and in part (d) the converse and the inverse were often confused.
A group of \(120\) women in the USA were asked whether they had visited the continents of Europe (\(E\)) or South America (\(S\)) or Asia (\(A\)).
\(7\) had visited all three continents
\(28\) had visited Europe only
\(22\) had visited South America only
\(16\) had visited Asia only
\(15\) had visited Europe and South America but had not visited Asia
\(x\) had visited South America and Asia but had not visited Europe
\(2x\) had visited Europe and Asia but had not visited South America
\(20\) had not visited any of these continents
Draw a Venn diagram, using sets labelled \(E\), \(S\) and \(A\), to show this information.
Calculate the value of \(x\).
Explain, in words, the meaning of \((E \cup S) \cap A'\).
Write down \(n\left( {(E \cup S \cup A)'} \right)\).
Find the probability that a woman selected at random from the group had visited Europe.
Find the probability that a woman selected at random from the group had visited Europe, given that she had visited Asia.
Two women from the group are selected at random.
Find the probability that both women selected had visited South America.
Markscheme
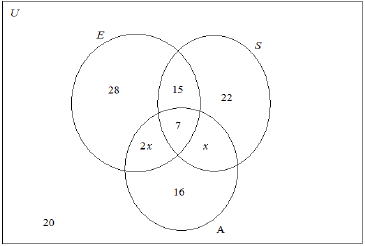 (A1)(A1)(A1)(A1)(A1)
(A1)(A1)(A1)(A1)(A1)
Notes: Award (A1) for rectangle and three labelled intersecting circles.
Award (A1) for \(7\) in correct place.
Award (A1) for \(28\), \(22\) and \(16\) in the correct places.
Award (A1) for \(15\), \(x\) and \(2x\) in the correct places.
Award (A1) for \(20\) in the correct place.
Accept \(4\) and \(8\) instead of \(x\) and \(2x\).
Do not penalize if \(U\) is omitted from the diagram.
[5 marks]
\(3x = 120 - (20 + 28 + 15 + 22 + 7 + 16)\) (M1)
Note: Award (M1) for setting up a correct equation involving \(x\), the \(120\) and values from their diagram.
\(x = 4\) (A1)(ft)(G2)
Note: Follow through from part (a). For the follow through to be awarded \(x\) must be a positive integer.
[2 marks]
(Women who had visited) Europe or South America and (but had) not (visited) Asia (A1)(A1)
Notes: Award (A1) for “(visited) Europe or South America” (or both).
Award (A1) for “and (but) had not visited Asia”.
\(E\)(urope) union \(S\)(outh America) intersected with not \(A\)(sia) earns no marks, (A0).
[2 marks]
\(20\) (A1)
Note: Award (A0) for the embedded answer of \(n(20)\).
[1 mark]
\(\frac{{58}}{{120}}{\text{ }}\left( {\frac{{29}}{{60}},{\text{ 0.483, 48.3% }}} \right){\text{ (0.48333}} \ldots {\text{)}}\) (A1)(ft)(A1)(G2)
Note: Award (A1)(ft) for numerator, follow through from their value of \(x\), or their diagram, (A1) for denominator.
[2 marks]
\(\frac{{15}}{{35}}{\text{ }}\left( {\frac{3}{7},{\text{ 0.429, 42.9% }}} \right){\text{ (0.428571}} \ldots {\text{)}}\) (A1)(ft)(A1)(ft)(G2)
Note: Award (A1)(ft) for numerator, (A1)(ft) for denominator, follow through from their value of \(x\) or their diagram.
[2 marks]
\(\frac{{48}}{{120}} \times \frac{{47}}{{119}}\) (A1)(ft)(M1)
Notes: Award (A1)(ft) for two correct fractions, follow through from their denominator in part (e), follow through the numerator from their answer to part (b) or from their diagram, (M1) for multiplication of their two fractions.
\( = \frac{{2256}}{{14\,280}}\left( {\frac{{94}}{{595}},{\text{ 0.158, 15,8% }}} \right){\text{ (0.157983}} \ldots {\text{)}}\) (A1)(ft)(G2)
Notes: Award (A1)(M1)(A1) for correct fractions, correctly multiplied together with an answer of \(0.16\).
Award (A0)(M1)(A0) for \(\frac{{48}}{{120}} \times \frac{{48}}{{120}} = 0.16\).
Award (G1) for an answer of \(0.16\) with no working seen.
[3 marks]
Examiners report
Candidates seemed to be well-drilled in the technique of creating Venn diagrams and using the data from their diagrams to solve problems in probability and this question was well answered. Except for the odd mistake in determining the value of x in part (b), many candidates scored full marks on the first two parts of the question. Indeed, those who calculated an incorrect value of x were able to recover many of the marks in the remainder of the question with the use of follow through marks. ‘Explain in words…’ required candidates to answer part (c) in the context of the question so ‘E union S intersection not A’ earned no marks. Of those candidates who did answer in context, many scored 1 mark for ‘had not visited Asia’ but a significant number used ‘and’ rather than ‘or’ and consequently were not awarded the other mark for expressing \(E \cup S\) in words. Whilst many correct answers of 20 were seen for part (d), a significant number of candidates wrote down the incorrect value of 113 which presumably was arrived at by evaluating \(n((E \cap S \cap A)')\) rather than the actual demand of the question. Having a Venn diagram seemed to be a good aid for parts (e) and (f) and much good work was seen in these two parts. However, in part (g), a significant number of candidates either chose a “with replacement” method or simply did not know what to do with the probabilities once they were found. As a consequence, this part of the question proved to be quite a discriminator.
Candidates seemed to be well-drilled in the technique of creating Venn diagrams and using the data from their diagrams to solve problems in probability and this question was well answered. Except for the odd mistake in determining the value of x in part (b), many candidates scored full marks on the first two parts of the question. Indeed, those who calculated an incorrect value of x were able to recover many of the marks in the remainder of the question with the use of follow through marks. ‘Explain in words…’ required candidates to answer part (c) in the context of the question so ‘E union S intersection not A’ earned no marks. Of those candidates who did answer in context, many scored 1 mark for ‘had not visited Asia’ but a significant number used ‘and’ rather than ‘or’ and consequently were not awarded the other mark for expressing \(E \cup S\) in words. Whilst many correct answers of 20 were seen for part (d), a significant number of candidates wrote down the incorrect value of 113 which presumably was arrived at by evaluating \(n((E \cap S \cap A)')\) rather than the actual demand of the question. Having a Venn diagram seemed to be a good aid for parts (e) and (f) and much good work was seen in these two parts. However, in part (g), a significant number of candidates either chose a “with replacement” method or simply did not know what to do with the probabilities once they were found. As a consequence, this part of the question proved to be quite a discriminator.
Candidates seemed to be well-drilled in the technique of creating Venn diagrams and using the data from their diagrams to solve problems in probability and this question was well answered. Except for the odd mistake in determining the value of x in part (b), many candidates scored full marks on the first two parts of the question. Indeed, those who calculated an incorrect value of x were able to recover many of the marks in the remainder of the question with the use of follow through marks. ‘Explain in words…’ required candidates to answer part (c) in the context of the question so ‘E union S intersection not A’ earned no marks. Of those candidates who did answer in context, many scored 1 mark for ‘had not visited Asia’ but a significant number used ‘and’ rather than ‘or’ and consequently were not awarded the other mark for expressing \(E \cup S\) in words. Whilst many correct answers of 20 were seen for part (d), a significant number of candidates wrote down the incorrect value of 113 which presumably was arrived at by evaluating \(n((E \cap S \cap A)')\) rather than the actual demand of the question. Having a Venn diagram seemed to be a good aid for parts (e) and (f) and much good work was seen in these two parts. However, in part (g), a significant number of candidates either chose a “with replacement” method or simply did not know what to do with the probabilities once they were found. As a consequence, this part of the question proved to be quite a discriminator.
Candidates seemed to be well-drilled in the technique of creating Venn diagrams and using the data from their diagrams to solve problems in probability and this question was well answered. Except for the odd mistake in determining the value of x in part (b), many candidates scored full marks on the first two parts of the question. Indeed, those who calculated an incorrect value of x were able to recover many of the marks in the remainder of the question with the use of follow through marks. ‘Explain in words…’ required candidates to answer part (c) in the context of the question so ‘E union S intersection not A’ earned no marks. Of those candidates who did answer in context, many scored 1 mark for ‘had not visited Asia’ but a significant number used ‘and’ rather than ‘or’ and consequently were not awarded the other mark for expressing \(E \cup S\) in words. Whilst many correct answers of 20 were seen for part (d), a significant number of candidates wrote down the incorrect value of 113 which presumably was arrived at by evaluating \(n((E \cap S \cap A)')\) rather than the actual demand of the question. Having a Venn diagram seemed to be a good aid for parts (e) and (f) and much good work was seen in these two parts. However, in part (g), a significant number of candidates either chose a “with replacement” method or simply did not know what to do with the probabilities once they were found. As a consequence, this part of the question proved to be quite a discriminator.
Candidates seemed to be well-drilled in the technique of creating Venn diagrams and using the data from their diagrams to solve problems in probability and this question was well answered. Except for the odd mistake in determining the value of x in part (b), many candidates scored full marks on the first two parts of the question. Indeed, those who calculated an incorrect value of x were able to recover many of the marks in the remainder of the question with the use of follow through marks. ‘Explain in words…’ required candidates to answer part (c) in the context of the question so ‘E union S intersection not A’ earned no marks. Of those candidates who did answer in context, many scored 1 mark for ‘had not visited Asia’ but a significant number used ‘and’ rather than ‘or’ and consequently were not awarded the other mark for expressing \(E \cup S\) in words. Whilst many correct answers of 20 were seen for part (d), a significant number of candidates wrote down the incorrect value of 113 which presumably was arrived at by evaluating \(n((E \cap S \cap A)')\) rather than the actual demand of the question. Having a Venn diagram seemed to be a good aid for parts (e) and (f) and much good work was seen in these two parts. However, in part (g), a significant number of candidates either chose a “with replacement” method or simply did not know what to do with the probabilities once they were found. As a consequence, this part of the question proved to be quite a discriminator.
Candidates seemed to be well-drilled in the technique of creating Venn diagrams and using the data from their diagrams to solve problems in probability and this question was well answered. Except for the odd mistake in determining the value of x in part (b), many candidates scored full marks on the first two parts of the question. Indeed, those who calculated an incorrect value of x were able to recover many of the marks in the remainder of the question with the use of follow through marks. ‘Explain in words…’ required candidates to answer part (c) in the context of the question so ‘E union S intersection not A’ earned no marks. Of those candidates who did answer in context, many scored 1 mark for ‘had not visited Asia’ but a significant number used ‘and’ rather than ‘or’ and consequently were not awarded the other mark for expressing \(E \cup S\) in words. Whilst many correct answers of 20 were seen for part (d), a significant number of candidates wrote down the incorrect value of 113 which presumably was arrived at by evaluating \(n((E \cap S \cap A)')\) rather than the actual demand of the question. Having a Venn diagram seemed to be a good aid for parts (e) and (f) and much good work was seen in these two parts. However, in part (g), a significant number of candidates either chose a “with replacement” method or simply did not know what to do with the probabilities once they were found. As a consequence, this part of the question proved to be quite a discriminator.
Candidates seemed to be well-drilled in the technique of creating Venn diagrams and using the data from their diagrams to solve problems in probability and this question was well answered. Except for the odd mistake in determining the value of x in part (b), many candidates scored full marks on the first two parts of the question. Indeed, those who calculated an incorrect value of x were able to recover many of the marks in the remainder of the question with the use of follow through marks. ‘Explain in words…’ required candidates to answer part (c) in the context of the question so ‘E union S intersection not A’ earned no marks. Of those candidates who did answer in context, many scored 1 mark for ‘had not visited Asia’ but a significant number used ‘and’ rather than ‘or’ and consequently were not awarded the other mark for expressing \(E \cup S\) in words. Whilst many correct answers of 20 were seen for part (d), a significant number of candidates wrote down the incorrect value of 113 which presumably was arrived at by evaluating \(n((E \cap S \cap A)')\) rather than the actual demand of the question. Having a Venn diagram seemed to be a good aid for parts (e) and (f) and much good work was seen in these two parts. However, in part (g), a significant number of candidates either chose a “with replacement” method or simply did not know what to do with the probabilities once they were found. As a consequence, this part of the question proved to be quite a discriminator.
A group of 66 people went on holiday to Hawaii. During their stay, three trips were arranged: a boat trip (\(B\)), a coach trip (\(C\)) and a helicopter trip (\(H\)).
From this group of people:
| 3 | went on all three trips; |
| 16 | went on the coach trip only; |
| 13 | went on the boat trip only; |
| 5 | went on the helicopter trip only; |
| x | went on the coach trip and the helicopter trip but not the boat trip; |
| 2x | went on the boat trip and the helicopter trip but not the coach trip; |
| 4x | went on the boat trip and the coach trip but not the helicopter trip; |
| 8 | did not go on any of the trips. |
One person in the group is selected at random.
Draw a Venn diagram to represent the given information, using sets labelled \(B\), \(C\) and \(H\).
Show that \(x = 3\).
Write down the value of \(n(B \cap C)\).
Find the probability that this person
(i) went on at most one trip;
(ii) went on the coach trip, given that this person also went on both the helicopter trip and the boat trip.
Markscheme
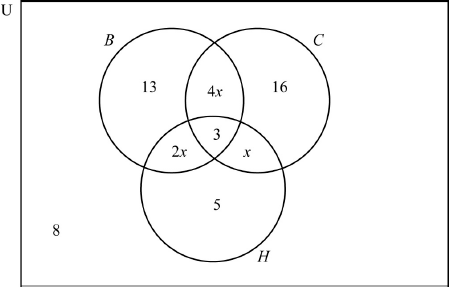 (A5)
(A5)
Notes: Award (A1) for rectangle and three labelled intersecting circles (U need not be seen),
(A1) for 3 in the correct region,
(A1) for 8 in the correct region,
(A1) for 5, 13 and 16 in the correct regions,
(A1) for \(x\), \(2x\) and \(4x\) in the correct regions.
[5 marks]
\(8 + 13 + 16 + 3 + 5 + x + 2x + 4x = 66\) (M1)
Note: Award (M1) for either a completely correct equation or adding all the terms from their diagram in part (a) and equating to 66.
Award (M0)(A0) if their equation has no \(x\).
\(7x = 66 - 45\) OR \(7x + 45 = 66\) (A1)
Note: Award (A1) for adding their like terms correctly, but only when the solution to their equation is equal to 3 and is consistent with their original equation.
\(x = 3\) (AG)
Note: The conclusion \(x = 3\) must be seen for the (A1) to be awarded.
[2 marks]
15 (A1)(ft)
Note: Follow through from part (a). The answer must be an integer.
[1 mark]
(i) \(\frac{{42}}{{66}}{\text{ }}\left( {\frac{7}{{11}},{\text{ }}0.636,{\text{ }}63.6\% } \right)\) (A1)(ft)(A1)(G2)
Note: Award (A1)(ft) for numerator, (A1) for denominator. Follow through from their Venn diagram.
(ii) \(\frac{3}{9}{\text{ }}\left( {\frac{1}{3},{\text{ }}0.333,{\text{ }}33.3\% } \right)\) (A1)(A1)(ft)(G2)
Note: Award (A1) for numerator, (A1)(ft) for denominator. Follow through from their Venn diagram.
[4 marks]
Examiners report
Mike, the laboratory mouse, is placed at the starting point, S, of a maze. Some paths in the maze lead to Trap A, some to Trap B, and others to escape doors. Some paths have one and some have two sections. If his path forks, Mike randomly chooses a path forward.
The following tree diagram represents the maze, showing all possible paths, and the probability that Mike chooses a certain section of a path through the maze.
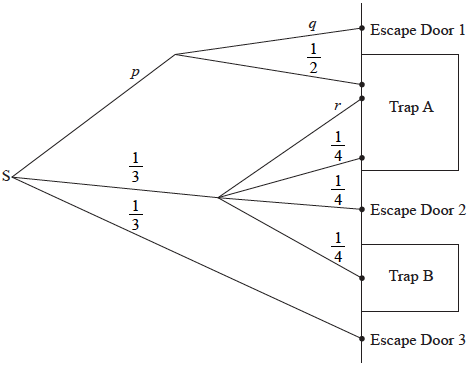
Write down the value of
(i) \(p\) ;
(ii) \(q\) ;
(iii) \(r\).
(i) Find the probability that Mike reaches Trap B.
(ii) Find the probability that Mike reaches Trap A.
(iii) Find the probability that Mike escapes from the maze.
Sonya, a lab assistant, counts the number of paths that lead to traps or escape doors. She believes that the probability that Mike will be trapped is greater than the probability that he will escape.
State whether Sonya is correct. Give a mathematical justification for your conclusion.
During the first trial Mike escapes.
Given that Mike escaped, find the probability that he went directly from S to Escape Door 3.
Markscheme
(i) \(\frac{1}{3}\;\;\;(0.333333…,{\text{ }}33.3333...\% )\) (A1)
(ii) \(\frac{1}{2}\;\;\;(0.5,{\text{ }}50\% )\) (A1)
(iii) \(\frac{1}{4}\;\;\;(0.25,{\text{ }}25\% )\) (A1)
(i) \(\frac{1}{3} \times \frac{1}{4}\) (M1)
\( = \frac{1}{{12}}\;\;\;({\text{0.0833333..., 8.33333...% )}}\) (A1)(G2)
(ii) \(\frac{1}{3} \times \frac{1}{2} + \frac{1}{3} \times \frac{1}{4} + \frac{1}{3} \times \frac{1}{4}\) (A1)(ft)(M1)
Note: Award (A1)(ft) for their three correct products seen, (M1) for addition of their products.
\( = \frac{1}{3}\;\;\;(0.333333...,{\text{ }}33.3333...\% )\) (A1)(ft)(G2)
Note: Follow through from their parts (a)(i) and (a)(iii).
(iii) \(1 - \frac{1}{{12}} - \frac{1}{3}\) (M1)
Note: Follow through from parts (b)(i) and (b)(ii).
OR
\(\frac{1}{3} \times \frac{1}{2} + \frac{1}{3} \times \frac{1}{4} + \frac{1}{3}\) (M1)
Note: Follow through from parts (a)(i) and (a)(ii).
\( = \frac{7}{{12}}\;\;\;(0.583333...,{\text{ }}58.3333...\% )\) (A1)(ft)(G2)
Sonya is not correct. (A1)(ft)
The probability that Mike escapes is \(\frac{7}{{12}}\), which is
greater than \(\frac{5}{{12}}{\text{ }}\left( {{\text{or greater than }}\frac{1}{2}} \right)\). (R1)(ft)
Notes: Do not award (A1)(R0).
Follow through from their answers to part (b).
\(\frac{{\frac{1}{3}}}{{\frac{7}{{12}}}}\) (A1)(A1)(ft)
Note: Award (A1) for correct numerator, (A1) for correct denominator.
\( = \frac{4}{7}\;\;\;\left( {\frac{{12}}{{21}},{\text{ 0.571428..., 57.1428...% }}} \right)\) (A1)(ft)(G2)
Note: Follow through from their answer to part (b)(iii).
Examiners report
A water container is made in the shape of a cylinder with internal height \(h\) cm and internal base radius \(r\) cm.
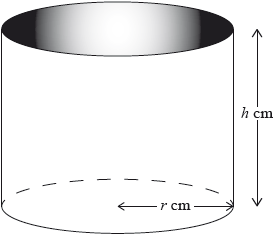
The water container has no top. The inner surfaces of the container are to be coated with a water-resistant material.
The volume of the water container is \(0.5{\text{ }}{{\text{m}}^3}\).
The water container is designed so that the area to be coated is minimized.
One can of water-resistant material coats a surface area of \(2000{\text{ c}}{{\text{m}}^2}\).
Write down a formula for \(A\), the surface area to be coated.
Express this volume in \({\text{c}}{{\text{m}}^3}\).
Write down, in terms of \(r\) and \(h\), an equation for the volume of this water container.
Show that \(A = \pi {r^2}\frac{{1\,000\,000}}{r}\).
Show that \(A = \pi {r^2} + \frac{{1\,000\,000}}{r}\).
Find \(\frac{{{\text{d}}A}}{{{\text{d}}r}}\).
Using your answer to part (e), find the value of \(r\) which minimizes \(A\).
Find the value of this minimum area.
Find the least number of cans of water-resistant material that will coat the area in part (g).
Markscheme
\((A = ){\text{ }}\pi {r^2} + 2\pi rh\) (A1)(A1)
Note: Award (A1) for either \(\pi {r^2}\) OR \(2\pi rh\) seen. Award (A1) for two correct terms added together.
[2 marks]
\(500\,000\) (A1)
Notes: Units not required.
[1 mark]
\(500\,000 = \pi {r^2}h\) (A1)(ft)
Notes: Award (A1)(ft) for \(\pi {r^2}h\) equating to their part (b).
Do not accept unless \(V = \pi {r^2}h\) is explicitly defined as their part (b).
[1 mark]
\(A = \pi {r^2} + 2\pi r\left( {\frac{{500\,000}}{{\pi {r^2}}}} \right)\) (A1)(ft)(M1)
Note: Award (A1)(ft) for their \({\frac{{500\,000}}{{\pi {r^2}}}}\) seen.
Award (M1) for correctly substituting only \({\frac{{500\,000}}{{\pi {r^2}}}}\) into a correct part (a).
Award (A1)(ft)(M1) for rearranging part (c) to \(\pi rh = \frac{{500\,000}}{r}\) and substituting for \(\pi rh\) in expression for \(A\).
\(A = \pi {r^2} + \frac{{1\,000\,000}}{r}\) (AG)
Notes: The conclusion, \(A = \pi {r^2} + \frac{{1\,000\,000}}{r}\), must be consistent with their working seen for the (A1) to be awarded.
Accept \({10^6}\) as equivalent to \({1\,000\,000}\).
[2 marks]
\(A = \pi {r^2} + 2\pi r\left( {\frac{{500\,000}}{{\pi {r^2}}}} \right)\) (A1)(ft)(M1)
Note: Award (A1)(ft) for their \({\frac{{500\,000}}{{\pi {r^2}}}}\) seen.
Award (M1) for correctly substituting only \({\frac{{500\,000}}{{\pi {r^2}}}}\) into a correct part (a).
Award (A1)(ft)(M1) for rearranging part (c) to \(\pi rh = \frac{{500\,000}}{r}\) and substituting for \(\pi rh\) in expression for \(A\).
\(A = \pi {r^2} + \frac{{1\,000\,000}}{r}\) (AG)
Notes: The conclusion, \(A = \pi {r^2} + \frac{{1\,000\,000}}{r}\), must be consistent with their working seen for the (A1) to be awarded.
Accept \({10^6}\) as equivalent to \({1\,000\,000}\).
[2 marks]
\(2\pi r - \frac{{{\text{1}}\,{\text{000}}\,{\text{000}}}}{{{r^2}}}\) (A1)(A1)(A1)
Note: Award (A1) for \(2\pi r\), (A1) for \(\frac{1}{{{r^2}}}\) or \({r^{ - 2}}\), (A1) for \( - {\text{1}}\,{\text{000}}\,{\text{000}}\).
[3 marks]
\(2\pi r - \frac{{1\,000\,000}}{{{r^2}}} = 0\) (M1)
Note: Award (M1) for equating their part (e) to zero.
\({r^3} = \frac{{1\,000\,000}}{{2\pi }}\) OR \(r = \sqrt[3]{{\frac{{1\,000\,000}}{{2\pi }}}}\) (M1)
Note: Award (M1) for isolating \(r\).
OR
sketch of derivative function (M1)
with its zero indicated (M1)
\((r = ){\text{ }}54.2{\text{ }}({\text{cm}}){\text{ }}(54.1926 \ldots )\) (A1)(ft)(G2)
[3 marks]
\(\pi {(54.1926 \ldots )^2} + \frac{{1\,000\,000}}{{(54.1926 \ldots )}}\) (M1)
Note: Award (M1) for correct substitution of their part (f) into the given equation.
\( = 27\,700{\text{ }}({\text{c}}{{\text{m}}^2}){\text{ }}(27\,679.0 \ldots )\) (A1)(ft)(G2)
[2 marks]
\(\frac{{27\,679.0 \ldots }}{{2000}}\) (M1)
Note: Award (M1) for dividing their part (g) by 2000.
\( = 13.8395 \ldots \) (A1)(ft)
Notes: Follow through from part (g).
14 (cans) (A1)(ft)(G3)
Notes: Final (A1) awarded for rounding up their \(13.8395 \ldots \) to the next integer.
[3 marks]
Examiners report
\(50\) students at Rambling High School were asked how they travelled to school yesterday. All of the students travelled by bus, by car or walked.
\(12\) students travelled by car only
\(7\) students travelled by bus only
\(5\) students travelled by car and walked, but did not use a bus
\(10\) students travelled by bus and walked, but did not use a car
\(3\) students used all three forms of travel.
Represent this information on a Venn Diagram.
There were \(28\) students who used a bus to travel to school. Calculate the number of students
(i) who travelled by car and by bus but did not walk;
(ii) who travelled by car.
Tomoko used a bus to travel to school yesterday.
Find the probability that she also walked.
Two students are chosen at random from all \(50\) students.
Find the probability that
(i) both students walked;
(ii) only one of the students walked.
Markscheme
(A4)
Note: Award (A1) for rectangle and three labelled intersecting circles, (A1) for \(3\), (A1) for \(5\) and \(10\), (A1) for \(7\) and \(12\).
(i) \(28 - (10 + 3 + 7) = 8\) (M1)(A1)(ft)(G2)
Note: Follow through from their Venn diagram.
(ii) \(5 + 3 + 8 + 12 = 28\) (M1)(A1)(ft)(G2)
Note: Follow through from part (b)(i) and their Venn diagram.
\({\text{P(}}\left. {{\text{walk}}} \right|{\text{bus}}) = \frac{{13}}{{28}}\) \((0.464{\text{, }}46.4\% )\) (\(0.464285 \ldots \)) (A1)(A1)(ft)(G2)
Note: Award (A1)(ft) for the numerator, (A1) for denominator.
(i) \(\frac{{23}}{{50}} \times \frac{{22}}{{49}}\) (A1)(M1)(M1)
Note: Award (A1) for \(23\) seen, (M1) for non replacement, (M1) for multiplying their fractions.
\( = \frac{{506}}{{2450}}\) \((0.207{\text{, }}20.7\% )\) (\(0.206530 \ldots \)) (A1)(G3)
(ii) \(\frac{{23}}{{50}} \times \frac{{27}}{{49}} + \frac{{27}}{{50}} \times \frac{{23}}{{49}}\) (A1)(ft)(M1)
Notes: Award (A1)(ft) for two products, (M1) for adding two products. Do not penalise in (ii) for consistent use of with replacement.
\( = \frac{{1242}}{{2450}}\) \((0.507{\text{, }}50.7\% )\) (\(0.509638 \ldots \)) (A1)(ft)(G2)
Examiners report
When Geraldine travels to work she can travel either by car (C), bus (B) or train (T). She travels by car on one day in five. She uses the bus 50 % of the time. The probabilities of her being late (L) when travelling by car, bus or train are 0.05, 0.12 and 0.08 respectively.
It is not necessary to use graph paper for this question.
Copy the tree diagram below and fill in all the probabilities, where NL represents not late, to represent this information.
Find the probability that Geraldine travels by bus and is late.
Find the probability that Geraldine is late.
Find the probability that Geraldine travelled by train, given that she is late.
Sketch the curve of the function \(f (x) = x^3 − 2x^2 + x − 3\) for values of \(x\) from −2 to 4, giving the intercepts with both axes.
On the same diagram, sketch the line \(y = 7 − 2x\) and find the coordinates of the point of intersection of the line with the curve.
Find the value of the gradient of the curve where \(x = 1.7\) .
Markscheme
Award (A1) for 0.5 at B, (A1) for 0.3 at T, then (A1) for each correct pair. Accept fractions or percentages. (A5)
[5 marks]
0.06 (accept \(0.5 \times 0.12\) or 6%) (A1)(ft)
[1 mark]
for a relevant two-factor product, either \(C \times L\) or \(T \times L\) (M1)
for summing three two-factor products (M1)
\((0.2 \times 0.05 + 0.06 + 0.3 \times 0.08)\)
0.094 (A1)(ft)(G2)
[3 marks]
\(\frac{{0.3 \times 0.08}}{{0.094}}\) (M1)(A1)(ft)
award (M1) for substituted conditional probability formula seen, (A1)(ft) for correct substitution
= 0.255 (A1)(ft)(G2)
[3 marks]
(G3)
[3 marks]
line drawn with –ve gradient and +ve y-intercept (G1)
(2.45, 2.11) (G1)(G1)
[3 marks]
\(f ' (1.7) = 3(1.7)^2 - 4(1.7) + 1\) (M1)
award (M1) for substituting in their \(f' (x)\)
2.87 (A1)(G2)
[2 marks]
Examiners report
This should have been an easy first question but, even so, there were some candidates who were unable to fill in the tree diagram correctly let alone evaluate any probabilities. The majority of candidates were confident with answering parts (a), (b) and (c) but the conditional probability question was not well answered with few candidates managing to recognise that it was a conditional type.
This should have been an easy first question but, even so, there were some candidates who were unable to fill in the tree diagram correctly let alone evaluate any probabilities. The majority of candidates were confident with answering parts (a), (b) and (c) but the conditional probability question was not well answered with few candidates managing to recognise that it was a conditional type.
This should have been an easy first question but, even so, there were some candidates who were unable to fill in the tree diagram correctly let alone evaluate any probabilities. The majority of candidates were confident with answering parts (a), (b) and (c) but the conditional probability question was not well answered with few candidates managing to recognise that it was a conditional type.
This should have been an easy first question but, even so, there were some candidates who were unable to fill in the tree diagram correctly let alone evaluate any probabilities. The majority of candidates were confident with answering parts (a), (b) and (c) but the conditional probability question was not well answered with few candidates managing to recognise that it was a conditional type.
This should have been an easy first question but, even so, there were some candidates who were unable to fill in the tree diagram correctly let alone evaluate any probabilities. The majority of candidates were confident with answering parts (a), (b) and (c) but the conditional probability question was not well answered with few candidates managing to recognise that it was a conditional type.
The curve sketching and straight line were well drawn but not all candidates indicated the intersection points with the axes. In finding the line / curve intersection some candidates did not use the intersection function on the GDC. Few candidates managed the last part. Many just chose two sets of coordinates and used the gradient formula.
This should have been an easy first question but, even so, there were some candidates who were unable to fill in the tree diagram correctly let alone evaluate any probabilities. The majority of candidates were confident with answering parts (a), (b) and (c) but the conditional probability question was not well answered with few candidates managing to recognise that it was a conditional type.
The curve sketching and straight line were well drawn but not all candidates indicated the intersection points with the axes. In finding the line / curve intersection some candidates did not use the intersection function on the GDC. Few candidates managed the last part. Many just chose two sets of coordinates and used the gradient formula.
This should have been an easy first question but, even so, there were some candidates who were unable to fill in the tree diagram correctly let alone evaluate any probabilities. The majority of candidates were confident with answering parts (a), (b) and (c) but the conditional probability question was not well answered with few candidates managing to recognise that it was a conditional type.
The curve sketching and straight line were well drawn but not all candidates indicated the intersection points with the axes. In finding the line / curve intersection some candidates did not use the intersection function on the GDC. Few candidates managed the last part. Many just chose two sets of coordinates and used the gradient formula.
100 students at IB College were asked whether they study Music (M), Chemistry (C), or Economics (E) with the following results.
10 study all three
15 study Music and Chemistry
17 study Music and Economics
12 study Chemistry and Economics
11 study Music only
6 study Chemistry only
Draw a Venn diagram to represent the information above.
Write down the number of students who study Music but not Economics.
There are 22 Economics students in total.
(i) Calculate the number of students who study Economics only.
(ii) Find the number of students who study none of these three subjects.
A student is chosen at random from the 100 that were asked above.
Find the probability that this student
(i) studies Economics;
(ii) studies Music and Chemistry but not Economics;
(iii) does not study either Music or Economics;
(iv) does not study Music given that the student does not study Economics.
Markscheme
(A1) for rectangle and three labelled circles (U need not be seen)
(A1) for 10 in the correct region
(A1) for 2, 7 and 5 in the correct regions
(A1) for 6 and 11 in the correct regions (A4)
16 (A1)(ft)
Note: Follow through from their Venn diagram.
(i) \(10 + 7 + 2\) (M1)
Note: Award (M1) for summing their 10, 7 and 2.
\(22 - 19\)
\(= 3\) (A1)(ft)(G2)
Note: Follow through from their diagram. Award (M1)(A1)(ft) for answers consistent with their diagram irrespective of whether working seen. Award a maximum of (M1)(A0) for a negative answer.
(ii) \(22 + 11+ 5 + 6\) (M1)
Note: Award (M1) for summing 22, and their 11, 5 and 6.
\(100 - 44\)
\(= 56\) (A1)(ft)(G2)
Note: Follow through from their diagram. Award (M1)(A1)(ft) for answers consistent with their diagram and the use of 22 irrespective of whether working seen. If negative values are used or implied award (M0)(A0).
(i) \(\frac{{22}}{{100}}\left( {\frac{{11}}{{50}},0.22,22\% } \right)\) (A1)(G1)
(ii) \(\frac{{5}}{{100}}\left( {\frac{{1}}{{20}},0.05,5\% } \right)\) (A1)(ft)(A1)(G2)
Note: Award (A1)(ft) for their 5 in numerator, (A1) for denominator.
Follow through from their diagram.
(iii) \(\frac{{62}}{{100}}\left( {\frac{{31}}{{50}},0.62,62\% } \right)\) (A1)(ft)(A1)(G2)
Note: Award (A1)(ft) for \(100 - (22 + 11 + {\text{their }}5)\), (A1) for denominator.
Follow through from their diagram.
(iv) \(\frac{{62}}{{78}}\left( {\frac{{31}}{{39}},0.795,79.5\% } \right)\) (0.794871...) (A1)(ft)(A1)(G2)
Note: Award (A1)(ft) for numerator, (A1) for denominator. Follow
through from part (d)(iii) for numerator.
Examiners report
This question divided the candidates into two parts: those who knew how to interpret the information in a manner the led to a consistent Venn diagram and those who did not. The use of the word “only” is crucial in this regard.
Follow through to the probability part of the question was contingent on the use of the given \(n(E) = 22\) ; given information should be used in subsequent parts. As ever, conditional probability proves a trial for many.
It is recommended that candidates write probabilities as unsimplified fractions as this increase their chances of gaining follow through from previous parts.
This question divided the candidates into two parts: those who knew how to interpret the information in a manner the led to a consistent Venn diagram and those who did not. The use of the word “only” is crucial in this regard.
Follow through to the probability part of the question was contingent on the use of the given \(n(E) = 22\) ; given information should be used in subsequent parts. As ever, conditional probability proves a trial for many.
It is recommended that candidates write probabilities as unsimplified fractions as this increase their chances of gaining follow through from previous parts.
This question divided the candidates into two parts: those who knew how to interpret the information in a manner the led to a consistent Venn diagram and those who did not. The use of the word “only” is crucial in this regard.
Follow through to the probability part of the question was contingent on the use of the given \(n(E) = 22\) ; given information should be used in subsequent parts. As ever, conditional probability proves a trial for many.
It is recommended that candidates write probabilities as unsimplified fractions as this increase their chances of gaining follow through from previous parts.
This question divided the candidates into two parts: those who knew how to interpret the information in a manner the led to a consistent Venn diagram and those who did not. The use of the word “only” is crucial in this regard.
Follow through to the probability part of the question was contingent on the use of the given \(n(E) = 22\) ; given information should be used in subsequent parts. As ever, conditional probability proves a trial for many.
It is recommended that candidates write probabilities as unsimplified fractions as this increase their chances of gaining follow through from previous parts.
Jorge conducted a survey of \(200\) drivers. He asked two questions:
How long have you had your driving licence?
Do you wear a seat belt when driving?
The replies are summarized in the table below.
Jorge applies a \({\chi ^2}\) test at the \(5\% \) level to investigate whether wearing a seat belt is associated with the time a driver has had their licence.
(i) Write down the null hypothesis, \({{\text{H}}_0}\).
(ii) Write down the number of degrees of freedom.
(iii) Show that the expected number of drivers that wear a seat belt and have had their driving licence for more than \(15\) years is \(22\), correct to the nearest whole number.
(iv) Write down the \({\chi ^2}\) test statistic for this data.
(v) Does Jorge accept \({{\text{H}}_0}\) ? Give a reason for your answer.
Consider the \(200\) drivers surveyed. One driver is chosen at random. Calculate the probability that
(i) this driver wears a seat belt;
(ii) the driver does not wear a seat belt, given that the driver has held a licence for more than \(15\) years.
Two drivers are chosen at random. Calculate the probability that
(i) both wear a seat belt.
(ii) at least one wears a seat belt.
Markscheme
(i) \({{\text{H}}_0} = \) wearing of a seat belt and the time a driver has held a licence are independent. (A1)
Note: For independent accept 'not associated' but do not accept 'not related' or 'not correlated'
(ii) \(2\) (A1)
(iii) \(\frac{{98 \times 45}}{{200}} = 22.05 = 22\) (correct to the nearest whole number) (M1)(A1)(AG)
Note: (M1) for correct formula and (A1) for correct substitution. Unrounded answer must be seen for the (A1) to be awarded.
(iv) \({\chi ^2} = 8.12\) (G2)
Note: For unrounded answer award (G1)(G0)(AP). If formula used award (M1) for correct substituted formula with correct substitution (6 terms) (A1) for correct answer.
(v) “Does not accept \({{\text{H}}_0}\)” (A1)(ft)
\(p{\text{-}}value < 0.05\) (R1)(ft)
Note: Allow “Reject \({{\text{H}}_0}\)” or equivalent. Follow through from their \({\chi ^2}\) statistic. Award (R1)(ft) for comparing the appropriate values. The (A1)(ft) can be awarded only if the conclusion is valid according to the comparison given. If no reason given or if reason is wrong the two marks are lost.
[8 marks]
(i) \(\frac{{98}}{{200}}( = 0.49{\text{, }}49\% )\) (A1)(A1)(G2)
Note: (A1) for numerator, (A1) for denominator.
(ii) \(\frac{{15}}{{45}}( = 0.333{\text{, }}33.3\% )\) (A1)(A1)(G2)
Note: (A1) for numerator, (A1) for denominator.
[4 marks]
(i) \(\frac{{98}}{{200}} \times \frac{{97}}{{199}} = 0.239{\text{ }}(23.9\% )\) (A1)(M1)(A1)(G3)
Note: (A1) for correct probabilities seen, (M1) for multiplying two probabilities, (A1) for correct answer.
(ii) \(1 - \frac{{102}}{{200}} \times \frac{{101}}{{199}} = 0.741{\text{ }}(74.1\% )\) (M1)(M1)(A1)(ft)(G2)
Note: (M1) for showing the product, (M1) for using the probability of the complement, (A1) for correct answer. Follow through for consistent use of with replacement.
OR
\(\frac{{98}}{{200}} \times \frac{{97}}{{199}} + \frac{{98}}{{200}} \times \frac{{102}}{{199}} + \frac{{102}}{{200}} \times \frac{{98}}{{199}} = 0.741{\text{ }}(74.1\% )\) (M1)(M1)(A1)(ft)(G2)
Note: (M1) for adding three products of fractions (or equivalent), (M1) for using the correct fractions, (A1) for correct answer. Follow through for consistent use of with replacement.
[6 marks]
Examiners report
The first part of the question was relatively well done. The null hypothesis and the degrees of freedom were well answered by the majority of the students. In the show that question some students used the GDC to find the expected values table and highlighted the correct value \(22.05\). This procedure gained no mark; the expected value formula was expected to be used here. Also those who did use the formula were expected to show the unrounded value \(22.05\) to gain full marks in this part question. Many lost the answer mark for not doing so. GDC was used by most of the students to find the chi-squared test though some students attempted to find this value by hand which made them waste time. Correct values were compared when deciding whether to accept or not the null hypothesis and follow through marks were awarded from their degrees of freedom and chi-squared test when incorrect.
The second part was not as successful as the first one. Simple probability was well answered. Not all the students changed the denominator to \(45\) for the second probability showing their weaknesses in conditional probability. It would have been useful for the students to use a tree diagram to help them solve the last part of this question but very few did so. Some of those students that reached the last part of the question forgot to add one of the three terms. Very few used the probability of the complement.
The first part of the question was relatively well done. The null hypothesis and the degrees of freedom were well answered by the majority of the students. In the show that question some students used the GDC to find the expected values table and highlighted the correct value \(22.05\). This procedure gained no mark; the expected value formula was expected to be used here. Also those who did use the formula were expected to show the unrounded value \(22.05\) to gain full marks in this part question. Many lost the answer mark for not doing so. GDC was used by most of the students to find the chi-squared test though some students attempted to find this value by hand which made them waste time. Correct values were compared when deciding whether to accept or not the null hypothesis and follow through marks were awarded from their degrees of freedom and chi-squared test when incorrect.
The second part was not as successful as the first one. Simple probability was well answered. Not all the students changed the denominator to \(45\) for the second probability showing their weaknesses in conditional probability. It would have been useful for the students to use a tree diagram to help them solve the last part of this question but very few did so. Some of those students that reached the last part of the question forgot to add one of the three terms. Very few used the probability of the complement.
The first part of the question was relatively well done. The null hypothesis and the degrees of freedom were well answered by the majority of the students. In the show that question some students used the GDC to find the expected values table and highlighted the correct value \(22.05\). This procedure gained no mark; the expected value formula was expected to be used here. Also those who did use the formula were expected to show the unrounded value \(22.05\) to gain full marks in this part question. Many lost the answer mark for not doing so. GDC was used by most of the students to find the chi-squared test though some students attempted to find this value by hand which made them waste time. Correct values were compared when deciding whether to accept or not the null hypothesis and follow through marks were awarded from their degrees of freedom and chi-squared test when incorrect.
The second part was not as successful as the first one. Simple probability was well answered. Not all the students changed the denominator to \(45\) for the second probability showing their weaknesses in conditional probability. It would have been useful for the students to use a tree diagram to help them solve the last part of this question but very few did so. Some of those students that reached the last part of the question forgot to add one of the three terms. Very few used the probability of the complement.
In a college 450 students were surveyed with the following results
150 have a television
205 have a computer
220 have an iPhone
75 have an iPhone and a computer
60 have a television and a computer
70 have a television and an iPhone
40 have all three.
Draw a Venn diagram to show this information. Use T to represent the set of students who have a television, C the set of students who have a computer and I the set of students who have an iPhone.
Write down the number of students that
(i) have a computer only;
(ii) have an iPhone and a computer but no television.
Write down \(n[T \cap (C \cup I)']\).
Calculate the number of students who have none of the three.
Two students are chosen at random from the 450 students. Calculate the probability that
(i) neither student has an iPhone;
(ii) only one of the students has an iPhone.
The students are asked to collect money for charity. In the first month, the students collect x dollars and the students collect y dollars in each subsequent month. In the first 6 months, they collect 7650 dollars. This can be represented by the equation x + 5y = 7650.
In the first 10 months they collect 13 050 dollars.
(i) Write down a second equation in x and y to represent this information.
(ii) Write down the value of x and of y .
The students are asked to collect money for charity. In the first month, the students collect x dollars and the students collect y dollars in each subsequent month. In the first 6 months, they collect 7650 dollars. This can be represented by the equation x + 5y = 7650.
In the first 10 months they collect 13 050 dollars.
Calculate the number of months that it will take the students to collect 49 500 dollars.
Markscheme
(A1)(A1)(A1)(A1)
Notes: Award (A1) for labelled sets T, C, and I included inside an enclosed universal set. (Label U is not essential.) Award (A1) for central entry 40. (A1) for 20, 30 and 35 in the other intersecting regions. (A1) for 60, 110 and 115 or T(150), C(205), I(220).
[4 marks]
In parts (b), (c) and (d) follow through from their diagram.
(i) 110 (A1)(ft)
(ii) 35 (A1)(ft)
[2 marks]
In parts (b), (c) and (d) follow through from their diagram.
60 (A1)(ft)
[2 marks]
In parts (b), (c) and (d) follow through from their diagram.
450 − (60 + 20 + 40 + 30 + 115 + 35 + 110) (M1)
Note: Award (M1) for subtracting all their values from 450.
= 40 (A1)(ft)(G2)
[2 marks]
(i) \(\frac{{230}}{{450}} \times \frac{{229}}{{449}}\) (A1)(M1)
Note: Award (A1) for correct fractions, (M1) for multiplying their fractions.
\(\frac{{52670}}{{202050}}\left( {\frac{{5267}}{{20205}},{\text{ 0}}{\text{.261, 26}}{\text{.1% }}} \right)(0.26067...)\) (A1)(G2)
Note: Follow through from their Venn diagram in part (a).
(ii) \(\frac{{220}}{{450}} \times \frac{{230}}{{449}} + \frac{{230}}{{450}} \times \frac{{220}}{{449}}\) (A1)(A1)
Note: Award (A1) for addition of their products, (A1) for two correct products.
OR
\(\frac{{230}}{{450}} \times \frac{{220}}{{449}} \times 2\) (A1)(A1)
Notes: Award (A1) for their product of two fractions multiplied by 2, (A1) for correct product of two fractions multiplied by 2. Award (A0)(A0) if correct product is seen not multiplied by 2.
\(\frac{{2024}}{{4041}}(0.501,{\text{ 50}}{\text{.1% )(0}}{\text{.50086}}...{\text{)}}\) (A1)(G2)
Note: Follow through from their Venn diagram in part (a) and/or their 230 used in part (e)(i).
Note: For consistent use of replacement in parts (i) and (ii) award at most (A0)(M1)(A0) in part (i) and (A1)(ft)(A1)(A1)(ft) in part (ii).
[6 marks]
(i) x + 9y = 13050 (A1)
(ii) x = 900 (A1)(ft)
y = 1350 (A1)(ft)
Notes: Follow through from their equation in (f)(i). Do not award (A1)(ft) if answer is negative. Award (M1)(A0) for an attempt at solving simultaneous equations algebraically but incorrect answer obtained.
[3 marks]
49500 = 900 + 1350n (A1)(ft)
Notes: Award (A1)(ft) for setting up correct equation. Follow through from candidate’s part (f).
n = 36 (A1)(ft)
The total number of months is 37. (A1)(ft)(G2)
Note: Award (G1) for 36 seen as final answer with no working. The value of n must be a positive integer for the last two (A1)(ft) to be awarded.
OR
49500 = 900 + 1350(n − 1) (A2)(ft)
Notes: Award (A2)(ft) for setting up correct equation. Follow through from candidate’s part (f).
n = 37 (A1)(ft)(G2)
Note: The value of n must be a positive integer for the last (A1)(ft) to be awarded.
[3 marks]
Examiners report
The question was moderately well answered. The majority of candidates answered part (a) and at least parts of (b), and (d).
The question was moderately well answered. The majority of candidates answered part (a) and at least parts of (b), and (d).
The question was moderately well answered. Part (c) proved to be difficult, as it required understanding and interpreting set notation.
The question was moderately well answered. The majority of candidates answered part (a) and at least parts of (b), and (d).
The question was moderately well answered. Part (e) was rarely answered in its entirety.
The question was moderately well answered. Part (f) was answered by many candidates, but most of them offered a partial answer to part (g); a typical response was 36 instead of 37.
The question was moderately well answered. Part (f) was answered by many candidates, but most of them offered a partial answer to part (g); a typical response was 36 instead of 37.
The figure below shows the lengths in centimetres of fish found in the net of a small trawler.
Find the total number of fish in the net.
Find (i) the modal length interval,
(ii) the interval containing the median length,
(iii) an estimate of the mean length.
(i) Write down an estimate for the standard deviation of the lengths.
(ii) How many fish (if any) have length greater than three standard deviations above the mean?
The fishing company must pay a fine if more than 10% of the catch have lengths less than 40cm.
Do a calculation to decide whether the company is fined.
A sample of 15 of the fish was weighed. The weight, W was plotted against length, L as shown below.
Exactly two of the following statements about the plot could be correct. Identify the two correct statements.
Note: You do not need to enter data in a GDC or to calculate r exactly.
(i) The value of r, the correlation coefficient, is approximately 0.871.
(ii) There is an exact linear relation between W and L.
(iii) The line of regression of W on L has equation W = 0.012L + 0.008 .
(iv) There is negative correlation between the length and weight.
(v) The value of r, the correlation coefficient, is approximately 0.998.
(vi) The line of regression of W on L has equation W = 63.5L + 16.5.
Markscheme
Total = 2 + 3 + 5 + 7 + 11 + 5 + 6 + 9 + 2 + 1 (M1)
(M1) is for a sum of frequencies.
= 51 (A1)(G2)
[2 marks]
Unit penalty (UP) is applicable where indicated in the left hand column.
(i) modal interval is 60 – 70
Award (A0) for 65 (A1)
(ii) median is length of fish no. 26, (M1)(A1)
also 60 – 70 (G2)
Can award (A1)(ft) or (G2)(ft) for 65 if (A0) was awarded for 65 in part (i).
(iii) mean is \(\frac{{2 \times 25 + 3 \times 35 + 5 \times 45 + 7 \times 55 + ...}}{{51}}\) (M1)
(UP) = 69.5 cm (3sf) (A1)(ft)(G1)
Note: (M1) is for a sum of (frequencies multiplied by midpoint values) divided by candidate’s answer from part (a). Accept mid-points 25.5, 35.5 etc or 24.5, 34.5 etc, leading to answers 70.0 or 69.0 (3sf) respectively. Answers of 69.0, 69.5 or 70.0 (3sf) with no working can be awarded (G1).
[5 marks]
Unit penalty (UP) is applicable where indicated in the left hand column.
(UP) (i) standard deviation is 21.8 cm (G1)
For any other answer without working, award (G0). If working is present then (G0)(AP) is possible.
(ii) \(69.5 + 3 \times 21.8 = 134.9 > 120\) (M1)
no fish (A1)(ft)(G1)
For ‘no fish’ without working, award (G1) regardless of answer to (c)(i). Follow through from (c)(i) only if method is shown.
[3 marks]
5 fish are less than 40 cm in length, (M1)
Award (M1) for any of \(\frac{5}{51}\), \(\frac{46}{51}\), 0.098 or 9.8%, 0.902, 90.2% or 5.1 seen.
hence no fine. (A1)(ft)
Note: There is no G mark here and (M0)(A1) is never allowed. The follow-through is from answer in part (a).
[2 marks]
(i) and (iii) are correct. (A1)(A1)
[2 marks]
Examiners report
a) b), c) There was much confusion about how to present the intervals. Often the mid-point only was seen. (eg. 65 instead of 60-70). Understanding of mode, median and mean was usually good but too many candidates wasted time calculating standard deviation by hand and got it wrong. In c(ii) 'greater than three' caused no problems but 'above the mean' was often ignored.
a) b), c) There was much confusion about how to present the intervals. Often the mid-point only was seen. (eg. 65 instead of 60-70). Understanding of mode, median and mean was usually good but too many candidates wasted time calculating standard deviation by hand and got it wrong. In c(ii) 'greater than three' caused no problems but 'above the mean' was often ignored.
a) b), c) There was much confusion about how to present the intervals. Often the mid-point only was seen. (eg. 65 instead of 60-70). Understanding of mode, median and mean was usually good but too many candidates wasted time calculating standard deviation by hand and got it wrong. In c(ii) 'greater than three' caused no problems but 'above the mean' was often ignored.
d) This was often well done, even if earlier parts were poorly done.
e) Rather mixed performance here. It was hard to identify any consistency in the errors made.
Too much time was spent on this question. It was only worth two marks and candidates ought to have realised that it relied on a general pictorial understanding of the concepts, possibly supplemented by a little elementary arithmetic only, to compare (iii) and (vi). With good understanding, many of the options could be ruled out in a few seconds.
Phoebe chooses a biscuit from a blue tin on a shelf. The tin contains one chocolate biscuit and four plain biscuits. She eats the biscuit and chooses another one from the tin. The tree diagram below represents the situation with the four possible outcomes where A stands for chocolate biscuit and B for plain biscuit.
On another shelf there are two tins, one red and one green. The red tin contains three chocolate biscuits and seven plain biscuits and the green tin contains one chocolate biscuit and four plain biscuits. Andrew randomly chooses either the red or the green tin and randomly selects a biscuit.
Write down the value of a.
Write down the value of b.
Find the probability that both biscuits are plain.
Copy and complete the tree diagram below.
Find the probability that he chooses a chocolate biscuit.
Find the probability that he chooses a biscuit from the red tin given that it is a chocolate biscuit.
Markscheme
a = 0 \(\left( {\frac{0}{4}} \right)\) (A1)
[1 mark]
\(b = \frac{3}{4}(0.75,{\text{ }}75\% )\) (A2)(G2)
[2 marks]
\(\frac{4}{5} \times \frac{3}{4}\) (M1)(A1)
\(\frac{{12}}{{20}}\left( {\frac{3}{5},{\text{ }}0.6,{\text{ 60% }}} \right)\) (A1)(ft)(G2)
Note: Award (M1) for multiplying two probabilities, (A1) for using their probabilities, (A1) for answer.
[3 marks]
(A1)(A1)(A1)
Note: Award (A1) for each pair.
[3 marks]
\(\frac{1}{2} \times \frac{3}{{10}} + \frac{1}{2} \times \frac{1}{5}\) (M1)(M1)
\( = \frac{5}{{20}}\left( {\frac{1}{4},{\text{ }}0.25,{\text{ 25% }}} \right)\) (A1)(ft)(G2)
Note: Award (M1) for two products seen with numbers from the problem, (M1) for adding two products. Follow through from their tree diagram.
[3 marks]
\(\frac{{\frac{1}{2} \times \frac{3}{{10}}}}{{\frac{1}{4}}}\) (M1)(A1)
\( = \frac{3}{5}{\text{ }}\left( {0.6,{\text{ 60 }}\% } \right)\) (A1)(ft)(G2)
Note: Award (M1) for substituted conditional probability formula, (A1) for correct substitution.
Follow through from their part (b) and part (c) (i).
[3 marks]
Examiners report
This question was well handled by most of the candidates except for (c)(ii) in which they had to find a conditional probability. Some candidates did not copy the second tree diagram in the answer sheets and instead wrote their answers in the exam booklet thus losing the 3 marks allocated to part (b).
This question was well handled by most of the candidates except for (c)(ii) in which they had to find a conditional probability. Some candidates did not copy the second tree diagram in the answer sheets and instead wrote their answers in the exam booklet thus losing the 3 marks allocated to part (b).
This question was well handled by most of the candidates except for (c)(ii) in which they had to find a conditional probability. Some candidates did not copy the second tree diagram in the answer sheets and instead wrote their answers in the exam booklet thus losing the 3 marks allocated to part (b).
This question was well handled by most of the candidates except for (c)(ii) in which they had to find a conditional probability. Some candidates did not copy the second tree diagram in the answer sheets and instead wrote their answers in the exam booklet thus losing the 3 marks allocated to part (b).
This question was well handled by most of the candidates except for (c)(ii) in which they had to find a conditional probability. Some candidates did not copy the second tree diagram in the answer sheets and instead wrote their answers in the exam booklet thus losing the 3 marks allocated to part (b).
This question was well handled by most of the candidates except for (c)(ii) in which they had to find a conditional probability. Some candidates did not copy the second tree diagram in the answer sheets and instead wrote their answers in the exam booklet thus losing the 3 marks allocated to part (b).
A store recorded their sales of televisions during the 2010 football World Cup. They looked at the numbers of televisions bought by gender and the size of the television screens.
This information is shown in the table below; S represents the size of the television screen in inches.
The store wants to use this information to predict the probability of selling these sizes of televisions for the 2014 football World Cup.
Use the table to find the probability that
(i) a television will be bought by a female;
(ii) a television with a screen size of 32 < S ≤ 46 will be bought;
(iii) a television with a screen size of 32 < S ≤ 46 will be bought by a female;
(iv) a television with a screen size greater than 46 inches will be bought, given that it is bought by a male.
The manager of the store wants to determine whether the screen size is independent of gender. A Chi-squared test is performed at the 1 % significance level.
Write down the null hypothesis.
The manager of the store wants to determine whether the screen size is independent of gender. A Chi-squared test is performed at the 1 % significance level.
Show that the expected frequency for females who bought a screen size of 32 < S ≤ 46, is 79, correct to the nearest integer.
The manager of the store wants to determine whether the screen size is independent of gender. A Chi-squared test is performed at the 1 % significance level.
Write down the number of degrees of freedom.
The manager of the store wants to determine whether the screen size is independent of gender. A Chi-squared test is performed at the 1 % significance level.
Write down the \({\chi ^2}\) calculated value.
The manager of the store wants to determine whether the screen size is independent of gender. A Chi-squared test is performed at the 1 % significance level.
Write down the critical value for this test.
The manager of the store wants to determine whether the screen size is independent of gender. A Chi-squared test is performed at the 1 % significance level.
Determine if the null hypothesis should be accepted. Give a reason for your answer.
Markscheme
(i) \(\frac{{220}}{{500}}\left( {\frac{{11}}{{25}},{\text{ 0}}{\text{.44, 44}}\% } \right)\) (A1)(G1)
(ii) \(\frac{{180}}{{500}}\left( {\frac{{9}}{{25}},{\text{ 0}}{\text{.36, 36}}\% } \right)\) (A1)(G1)
(iii) \(\frac{{40}}{{500}}\left( {\frac{{2}}{{25}},{\text{ 0}}{\text{.08, 8}}\% } \right)\) (A1)(A1)(G2)
(iv) \(\frac{{55}}{{500}}\left( {\frac{{11}}{{56}},{\text{ 0}}{\text{.196, 19.6}}\% } \right)\) (A1)(A1)(G2)
Note: Award (A1) for numerator, (A1) for denominator. Award (A0)(A0) if answers are given as incorrect reduced fractions without working.
[6 marks]
“The size of the television screen is independent of gender.” (A1)
Note: Accept “not associated”, do not accept “not correlated”.
[1 mark]
\(\frac{{180}}{{500}} \times \frac{{220}}{{500}} \times 500\) OR \(\frac{{180 \times 220}}{{500}}\) (M1)
= 79.2 (A1)
= 79 (AG)
Note: Both the unrounded and the given answer must be seen for the final (A1) to be awarded.
[2 marks]
3 (A1)
[1 mark]
\(\chi _{calc}^2\) = 104(103.957...) (G2)
Note: Award (M1) if an attempt at using the formula is seen but incorrect answer obtained.
[2 marks]
11.345 (A1)(ft)
Notes: Follow through from their degrees of freedom.
[1 mark]
\(\chi _{calc}^2\) > \(\chi _{crit}^2\) OR p < 0.01 (R1)
Do not accept H0. (A1)(ft)
Note: Do not award (R0)(A1)(ft). Follow through from their parts (d), (e) and (f).
[2 marks]
Examiners report
Part (a) was generally well answered by most of the students, except for part (a)(iv) which called for conditional probability.
Most students correctly stated the null hypothesis in part (b), and answered parts (d), (e), (f) and (g).
In some responses to part (c) it seemed that the difference between calculation of the expected value and showing that the value is 79 was not clear to the candidates. It is important that teachers explain to their students that in a “show that” question they are expected to demonstrate the mathematical reasoning through which the given answer is obtained.
Most students correctly stated the null hypothesis in part (b), and answered parts (d), (e), (f) and (g).
Most students correctly stated the null hypothesis in part (b), and answered parts (d), (e), (f) and (g).
Most students correctly stated the null hypothesis in part (b), and answered parts (d), (e), (f) and (g).
Most students correctly stated the null hypothesis in part (b), and answered parts (d), (e), (f) and (g).
A group of 50 students completed a questionnaire for a Mathematical Studies project. The following data was collected.
\(18\) students own a digital camera (D)
\(15\) students own an iPod (I)
\(26\) students own a cell phone (C)
\(1\) student owns all three items
\(5\) students own a digital camera and an iPod but not a cell phone
\(2\) students own a cell phone and an iPod but not a digital camera
\(3\) students own a cell phone and a digital camera but not an iPod
Claire and Kate both wish to go to the cinema but one of them has to stay at home to baby-sit.
The probability that Kate goes to the cinema is \(0.2\). If Kate does not go Claire goes.
If Kate goes to the cinema the probability that she is late home is \(0.3\).
If Claire goes to the cinema the probability that she is late home is \(0.6\).
Represent this information on a Venn diagram.
Calculate the number of students who own none of the items mentioned above.
If a student is chosen at random, write down the probability that the student owns a digital camera only.
If two students are chosen at random, calculate the probability that they both own a cell phone only.
If a student owns an iPod, write down the probability that the student also owns a digital camera.
Copy and complete the probability tree diagram below.
Calculate the probability that
(i) Kate goes to the cinema and is not late;
(ii) the person who goes to the cinema arrives home late.
Markscheme
(A1)(A1)(A1)(A1)(ft)
Note: (A1) for rectangle with 3 intersecting circles, (A1) for \(1\), (A1) for \(5\), \(3\), \(2\), (A1)(ft) for \(9\), \(7\), \(20\) if subtraction is carried out, or \(18\), \(15\), \(26\) seen by the letters D, I and C.
[4 marks]
\(50 - 47\) (M1)
Note: (M1) for subtracting their value from \(50\).
\( = 3\) (A1)(ft)(G2)
[2 marks]
\(\frac{9}{{50}}\) (A1)(ft)
[1 mark]
\(\frac{{20}}{{50}} \times \frac{{19}}{{49}}\) (A1)(ft)(M1)
\( = \frac{{38}}{{245}}{\text{ }}\left( {\frac{{380}}{{2450}}{\text{, }}0.155{\text{, }}15.5\% } \right)\) (A1)(ft)(G2)
Notes: (A1)(ft) for correct fractions from their Venn diagram
(M1) for multiplying their fractions
(A1)(ft) for correct answer.
[3 marks]
\(\frac{6}{{15}}{\text{ }}\left( {\frac{2}{5}{\text{, }}0.4{\text{, }}40\% } \right)\) (A1)(ft)(A1)(ft)
Note: (A1)(ft) for numerator, (A1)(ft) denominator.
[2 marks]
(A1)(A1)(A1)
Note: (A1) for \(0.8\), (A1) for \(0.7\), (A1) for \(0.6\) and \(0.4\).
[3 marks]
(i) \(0.2 \times 0.7 = 0.14\) (M1)(A1)(ft)(G2)
Note: (M1) for multiplying correct numbers.
[2 marks]
(ii) \(0.2 \times 0.3 + 0.8 \times 0.6\) (M1)(M1)
\( = 0.54\) (A1)(ft)(G3)
Note: (M1) for each correct product (use candidate’s tree), (A1)(ft) for answer.
[3 marks]
Examiners report
The Venn diagram was well drawn on the whole although some of the candidates missed out the Universal box and others filled in the intersections wrongly but still gained ft marks for the remaining parts of the question.
Well answered.
Well answered.
Few correct answers. Either candidates added instead of multiplying or they used replacement and so the fractions given were the same.
Again few correct answers. Candidates wrote the answer out of \(50\) instead of \(15\).
The tree diagram was well done on the whole. It appears as if some candidates may have completed this on the exam paper and this was not included with their papers. However, the question did state clearly “Copy and complete …”
(i) This part was well done by those candidates who remembered to multiply instead of add.
(ii) Many candidates just wrote down “Claire” for this answer. Others wrongly multiplied or added \(0.3\) with \(0.6\).
One day the numbers of customers at three cafés, “Alan’s Diner” ( \(A\) ), “Sarah’s Snackbar” ( \(S\) ) and “Pete’s Eats” ( \(P\) ), were recorded and are given below.
17 were customers of Pete’s Eats only
27 were customers of Sarah’s Snackbar only
15 were customers of Alan’s Diner only
10 were customers of Pete’s Eats and Sarah’s Snackbar but not Alan’s Diner
8 were customers of Pete’s Eats and Alan’s Diner but not Sarah’s Snackbar
Some of the customers in each café were given survey forms to complete to find out if they were satisfied with the standard of service they received.
Draw a Venn Diagram, using sets labelled \(A\) , \(S\) and \(P\) , that shows this information.
There were 48 customers of Pete’s Eats that day. Calculate the number of people who were customers of all three cafés.
There were 50 customers of Sarah’s Snackbar that day. Calculate the total number of people who were customers of Alan’s Diner.
Write down the number of customers of Alan’s Diner that were also customers of Pete’s Eats.
Find \(n[(S \cup P) \cap A']\).
One of the survey forms was chosen at random, find the probability that the form showed “Dissatisfied”;
One of the survey forms was chosen at random, find the probability that the form showed “Satisfied” and was completed at Sarah’s Snackbar;
One of the survey forms was chosen at random, find the probability that the form showed “Dissatisfied”, given that it was completed at Alan’s Diner.
A \({\chi ^2}\) test at the \(5\% \) significance level was carried out to determine whether there was any difference in the level of customer satisfaction in each of the cafés.
Write down the null hypothesis, \({{\text{H}}_0}\) , for the \({\chi ^2}\) test.
A \({\chi ^2}\) test at the \(5\% \) significance level was carried out to determine whether there was any difference in the level of customer satisfaction in each of the cafés.
Write down the number of degrees of freedom for the test.
A \({\chi ^2}\) test at the \(5\% \) significance level was carried out to determine whether there was any difference in the level of customer satisfaction in each of the cafés.
Using your graphic display calculator, find \({\chi ^2}_{calc}\) .
A \({\chi ^2}\) test at the \(5\% \) significance level was carried out to determine whether there was any difference in the level of customer satisfaction in each of the cafés.
State, giving a reason, the conclusion to the test.
Markscheme
(A1) for rectangle and three labelled intersecting circles
(A1) for \(15\), \(27\) and \(17\)
(A1) for \(10\) and \(8\) (A3)
[3 marks]
\(48 - (8 +10 +17)\) or equivalent (M1)
\( = 13\) (A1)(ft)(G2)
[2 marks]
\(50 - (27 +10 +13)\) (M1)
Note: Award (M1) for working seen.
\( = 0\) (A1)
number of elements in A \(= 36\) (A1)(ft)(G3)
Note: Follow through from (b).
[3 marks]
\(21\) (A1)(ft)
Note: Follow through from (b) even if no working seen.
[1 mark]
\(54\) (M1)(A1)(ft)(G2)
Note: Award (M1) for \(17\), \(10\), \(27\) seen. Follow through from (a).
[2 marks]
\(\frac{{40}}{{120}}{\text{ }}\left( {\frac{1}{3}{\text{, }}0.333{\text{, }}33.3\% } \right)\) (A1)(A1)(G2)
Note: Award (A1) for numerator, (A1) for denominator.
[2 marks]
\(\frac{{34}}{{120}}{\text{ }}\left( {\frac{{17}}{{60}}{\text{, }}0.283{\text{, }}28.3\% } \right)\) (A1)(A1)(G2)
Note: Award (A1) for numerator, (A1) for denominator.
[2 marks]
\(\frac{8}{{28}}{\text{ }}\left( {\frac{2}{7}{\text{, }}0.286{\text{, }}28.6\% } \right)\) (A1)(A1)(G2)
Note: Award (A1) for numerator, (A1) for denominator.
[2 marks]
customer satisfaction is independent of café (A1)
Note: Accept “customer satisfaction is not associated with the café”.
[1 mark]
\(2\) (A1)
[1 mark]
\(0.754\) (G2)
Note: Award (G1)(G1)(AP) for \(0.75\) or for correct answer incorrectly rounded to 3 s.f. or more, (G0) for \(0.7\).
[2 marks]
since \({\chi ^2}_{calc} < {\chi ^2}_{crit}5.991 accept (or Do not reject) H0 (R1)(A1)(ft)
Note: Follow through from their value in (e).
OR
Accept (or Do not reject) H0 as \(p\)-value \((0.686) > 0.05\) (R1)(A1)(ft)
Notes: Do not award (A1)(R0). Award the (R1) for comparison of appropriate values.
[2 marks]
Examiners report
Part A
This part was successfully attempted by the great majority. A common mistake was the failure to intersect all three sets.
Part A
This part was successfully attempted by the great majority. A common mistake was the failure to intersect all three sets.
Part A
This part was successfully attempted by the great majority. A common mistake was the failure to intersect all three sets.
Part A
This part was successfully attempted by the great majority. A common mistake was the failure to intersect all three sets.
Part A
This part was successfully attempted by the great majority. A common mistake was the failure to intersect all three sets.
A surprising number seemed unfamiliar with set notation in (e) and thus did not attempt this part.
Part B
The work on probability also proved accessible to the great majority with a large number of candidates attaining full marks. Most errors occurred due to candidates trying to use the algebraic form of laws of probability, rather than by interpreting the contingency table.
Part B
The work on probability also proved accessible to the great majority with a large number of candidates attaining full marks. Most errors occurred due to candidates trying to use the algebraic form of laws of probability, rather than by interpreting the contingency table.
Part B
The work on probability also proved accessible to the great majority with a large number of candidates attaining full marks. Most errors occurred due to candidates trying to use the algebraic form of laws of probability, rather than by interpreting the contingency table.
Part B
The work on probability also proved accessible to the great majority with a large number of candidates attaining full marks. Most errors occurred due to candidates trying to use the algebraic form of laws of probability, rather than by interpreting the contingency table.
The chi-squared test was well done by the great majority, however, it was clear that a number of centres do not teach this subject, since there were a number of scripts which either were left blank or showed no understanding in the responses seen.
Part B
The work on probability also proved accessible to the great majority with a large number of candidates attaining full marks. Most errors occurred due to candidates trying to use the algebraic form of laws of probability, rather than by interpreting the contingency table.
The chi-squared test was well done by the great majority, however, it was clear that a number of centres do not teach this subject, since there were a number of scripts which either were left blank or showed no understanding in the responses seen.
Part B
The work on probability also proved accessible to the great majority with a large number of candidates attaining full marks. Most errors occurred due to candidates trying to use the algebraic form of laws of probability, rather than by interpreting the contingency table.
The chi-squared test was well done by the great majority, however, it was clear that a number of centres do not teach this subject, since there were a number of scripts which either were left blank or showed no understanding in the responses seen.
Part B
The work on probability also proved accessible to the great majority with a large number of candidates attaining full marks. Most errors occurred due to candidates trying to use the algebraic form of laws of probability, rather than by interpreting the contingency table.
The chi-squared test was well done by the great majority, however, it was clear that a number of centres do not teach this subject, since there were a number of scripts which either were left blank or showed no understanding in the responses seen.
The Venn diagram below represents the students studying Mathematics (A), Further Mathematics (B) and Physics (C) in a school.
50 students study Mathematics
38 study Physics
20 study Mathematics and Physics but not Further Mathematics
10 study Further Mathematics but not Physics
12 study Further Mathematics and Physics
6 study Physics but not Mathematics
3 study none of these three subjects.
Three propositions are given as
p : It is snowing q : The roads are open r : We will go skiing
Copy and complete the Venn diagram on your answer paper.
Write down the number of students who study Mathematics but not Further Mathematics.
Write down the total number of students in the school.
Write down \(n({\text{B}} \cup {\text{C}})\).
Write the following compound statement in symbolic form.
“It is snowing and the roads are not open.”
Write the following compound statement in words.
\((\neg p \wedge q) \Rightarrow r\)
An incomplete truth table for the compound proposition \((\neg p \wedge q) \Rightarrow r\) is given below.
Copy and complete the truth table on your answer paper.
Markscheme
(A1)(A1)(A1)
Note: Award (A1) for each correct number in the correct position.
[3 marks]
28 (A1)(ft)
Note: 20 + their 8.
[1 mark]
59 (A1)(ft)
[1 mark]
10 + 12 + 20 + 6 (M1)
Note: Award (M1) for use of the correct regions.
= 48 (A1)(ft)(G2)
OR
59 − 8 − 3 (M1)
= 48 (A1)(ft)
[2 marks]
\(p \wedge \neg q\) (A1)(A1)
Note: Award (A1) for \(\wedge\), (A1) for both statements in the correct order.
[2 marks]
If it is not snowing and the roads are open (then) we will go skiing. (A1)(A1)(A1)
Note: Award (A1) for “if…(then)”, (A1) for “not snowing and the roads are open”, (A1) for “we will go skiing”.
[3 marks]
(A1)(A1)(ft)(A1)(ft)
Note: Award (A1) for each correct column.
[3 marks]
Examiners report
This part was successfully attempted by the great majority. The less familiar form of the Venn diagram seemed not to cause too many problems, although a common mistake was the failure to add the 20 in set A in part (b). A surprising number seemed unfamiliar with set notation in (d) and thus were not able to attempt this part.
This part was successfully attempted by the great majority. The less familiar form of the Venn diagram seemed not to cause too many problems, although a common mistake was the failure to add the 20 in set A in part (b). A surprising number seemed unfamiliar with set notation in (d) and thus were not able to attempt this part.
This part was successfully attempted by the great majority. The less familiar form of the Venn diagram seemed not to cause too many problems, although a common mistake was the failure to add the 20 in set A in part (b). A surprising number seemed unfamiliar with set notation in (d) and thus were not able to attempt this part.
This part was successfully attempted by the great majority. The less familiar form of the Venn diagram seemed not to cause too many problems, although a common mistake was the failure to add the 20 in set A in part (b). A surprising number seemed unfamiliar with set notation in (d) and thus were not able to attempt this part.
The work on logic also proved accessible to the great majority with a large number of candidates attaining full marks. The most common errors were the omission of the “If” in the conditional statement in (b) and the inability to follow the implication in the truth table in (c).
The work on logic also proved accessible to the great majority with a large number of candidates attaining full marks. The most common errors were the omission of the “If” in the conditional statement in (b) and the inability to follow the implication in the truth table in (c).
The work on logic also proved accessible to the great majority with a large number of candidates attaining full marks. The most common errors were the omission of the “If” in the conditional statement in (b) and the inability to follow the implication in the truth table in (c).
Part A
100 students are asked what they had for breakfast on a particular morning. There were three choices: cereal (X) , bread (Y) and fruit (Z). It is found that
10 students had all three
17 students had bread and fruit only
15 students had cereal and fruit only
12 students had cereal and bread only
13 students had only bread
8 students had only cereal
9 students had only fruit
Part B
The same 100 students are also asked how many meals on average they have per day. The data collected is organized in the following table.
A \({\chi ^2}\) test is carried out at the 5 % level of significance.
Represent this information on a Venn diagram.
Find the number of students who had none of the three choices for breakfast.
Write down the percentage of students who had fruit for breakfast.
Describe in words what the students in the set \(X \cap Y'\) had for breakfast.
Find the probability that a student had at least two of the three choices for breakfast.
Two students are chosen at random. Find the probability that both students had all three choices for breakfast.
Write down the null hypothesis, H0, for this test.
Write down the number of degrees of freedom for this test.
Write down the critical value for this test.
Show that the expected number of females that have more than 5 meals per day is 13, correct to the nearest integer.
Use your graphic display calculator to find the \(\chi _{calc}^2\) for this data.
Decide whether H0 must be accepted. Justify your answer.
Markscheme
(A1) for rectangle and three intersecting circles
(A1) for 10, (A1) for 8, 13 and 9, (A1) for 12, 15 and 17 (A4)
[4 marks]
100 – (9 +12 +13 +15 +10 +17 + 8) =16 (M1)(A1)(ft)(G2)
Note: Follow through from their diagram.
[2 marks]
\(\frac{{51}}{{100}}(0.51)\) (A1)(ft)
= 51% (A1)(ft)(G2)
Note: Follow through from their diagram.
[2 marks]
Note: The following statements are correct. Please note that the connectives are important. It is not the same (had cereal) and (not bread) and (had cereal) or (not bread). The parentheses are not needed but are there to facilitate the understanding of the propositions.
(had cereal) and (did not have bread)
(had cereal only) or (had cereal and fruit only)
(had either cereal or (fruit and cereal)) and (did not have bread) (A1)(A1)
Notes: If the statements are correct but the connectives are wrong then award at most (A1)(A0). For the statement (had only cereal) and (cereal and fruit) award (A1)(A0). For the statement had cereal and fruit award (A0)(A0).
[2 marks]
\(\frac{{54}}{{100}}(0.54,{\text{ 54 % }})\) (A1)(ft)(A1)(ft)(G2)
Note: Award (A1)(ft) for numerator, follow through from their diagram, (A1)(ft) for denominator. Follow through from total or denominator used in part (c).
[2 marks]
\(\frac{{10}}{{100}} \times \frac{9}{{99}} = \frac{1}{{110}}(0.00909,{\text{ 0}}{\text{.909 % }})\) (A1)(ft)(M1)(A1)(ft)(G2)
Notes: Award (A1)(ft) for their correct fractions, (M1) for multiplying two fractions, (A1)(ft) for their correct answer. Answer 0.009 with no working receives no marks. Follow through from denominator in parts (c) and (e) and from their diagram.
[3 marks]
H0 : The (average) number of meals per day a student has and gender are independent (A1)
Note: For “independent” accept “not associated” but do not accept “not related” or “not correlated”.
[1 mark]
2 (A1)
[1 mark]
5.99 (accept 5.991) (A1)(ft)
Note: Follow through from their part (b).
[1 mark]
\(\frac{{28 \times 45}}{{100}} = 12.6 = 13\) or \(\frac{{28}}{{100}} \times \frac{{25}}{{100}} \times 100 = 12.6 = 13\) (M1)(A1)(AG)
Notes: Award (M1) for correct formula and (A1) for correct substitution. Unrounded answer must be seen for the (A1) to be awarded.
[2 marks]
0.0321 (G2)
Note: For 0.032 award (G1)(G1)(AP). For 0.03 with no working award (G0).
[2 marks]
0.0321 < 5.99 or 0.984 > 0.05 (R1)
accept H0 (A1)(ft)
Note: If reason is incorrect both marks are lost, do not award (R0)(A1).
[2 marks]
Examiners report
This question was in general well done. Candidates began the paper well by drawing the Venn diagram correctly. Some students omitted the rectangle (universal set) around the three circles. There were quite a few errors in (c) as some students forgot to convert their answers to percentages. Also describing in words what the students in \(X \cap Y'\) had for breakfast seemed to be difficult for the majority of the candidates. Some misread what Y was and even more missed the complement sign. However, the main problem in answering this question seemed to be the lack of knowledge in the relationship between set theory and logic (use of "and" and "or"). Combining probabilities caused problems to many. Common wrong answers were \(\frac{{10}}{{100}}\), \(\frac{{10}}{{100}} \times \frac{{10}}{{100}}\) or \(\frac{{10}}{{100}} + \frac{9}{{99}}\).
This question was in general well done. Candidates began the paper well by drawing the Venn diagram correctly. Some students omitted the rectangle (universal set) around the three circles. There were quite a few errors in (c) as some students forgot to convert their answers to percentages. Also describing in words what the students in \(X \cap Y'\) had for breakfast seemed to be difficult for the majority of the candidates. Some misread what Y was and even more missed the complement sign. However, the main problem in answering this question seemed to be the lack of knowledge in the relationship between set theory and logic (use of "and" and "or"). Combining probabilities caused problems to many. Common wrong answers were \(\frac{{10}}{{100}}\), \(\frac{{10}}{{100}} \times \frac{{10}}{{100}}\) or \(\frac{{10}}{{100}} + \frac{9}{{99}}\).
This question was in general well done. Candidates began the paper well by drawing the Venn diagram correctly. Some students omitted the rectangle (universal set) around the three circles. There were quite a few errors in (c) as some students forgot to convert their answers to percentages. Also describing in words what the students in \(X \cap Y'\) had for breakfast seemed to be difficult for the majority of the candidates. Some misread what Y was and even more missed the complement sign. However, the main problem in answering this question seemed to be the lack of knowledge in the relationship between set theory and logic (use of "and" and "or"). Combining probabilities caused problems to many. Common wrong answers were \(\frac{{10}}{{100}}\), \(\frac{{10}}{{100}} \times \frac{{10}}{{100}}\) or \(\frac{{10}}{{100}} + \frac{9}{{99}}\).
This question was in general well done. Candidates began the paper well by drawing the Venn diagram correctly. Some students omitted the rectangle (universal set) around the three circles. There were quite a few errors in (c) as some students forgot to convert their answers to percentages. Also describing in words what the students in \(X \cap Y'\) had for breakfast seemed to be difficult for the majority of the candidates. Some misread what Y was and even more missed the complement sign. However, the main problem in answering this question seemed to be the lack of knowledge in the relationship between set theory and logic (use of "and" and "or"). Combining probabilities caused problems to many. Common wrong answers were \(\frac{{10}}{{100}}\), \(\frac{{10}}{{100}} \times \frac{{10}}{{100}}\) or \(\frac{{10}}{{100}} + \frac{9}{{99}}\).
This question was in general well done. Candidates began the paper well by drawing the Venn diagram correctly. Some students omitted the rectangle (universal set) around the three circles. There were quite a few errors in (c) as some students forgot to convert their answers to percentages. Also describing in words what the students in \(X \cap Y'\) had for breakfast seemed to be difficult for the majority of the candidates. Some misread what Y was and even more missed the complement sign. However, the main problem in answering this question seemed to be the lack of knowledge in the relationship between set theory and logic (use of "and" and "or"). Combining probabilities caused problems to many. Common wrong answers were \(\frac{{10}}{{100}}\), \(\frac{{10}}{{100}} \times \frac{{10}}{{100}}\) or \(\frac{{10}}{{100}} + \frac{9}{{99}}\).
This question was in general well done. Candidates began the paper well by drawing the Venn diagram correctly. Some students omitted the rectangle (universal set) around the three circles. There were quite a few errors in (c) as some students forgot to convert their answers to percentages. Also describing in words what the students in \(X \cap Y'\) had for breakfast seemed to be difficult for the majority of the candidates. Some misread what Y was and even more missed the complement sign. However, the main problem in answering this question seemed to be the lack of knowledge in the relationship between set theory and logic (use of "and" and "or"). Combining probabilities caused problems to many. Common wrong answers were \(\frac{{10}}{{100}}\), \(\frac{{10}}{{100}} \times \frac{{10}}{{100}}\) or \(\frac{{10}}{{100}} + \frac{9}{{99}}\).
In general this part question was well answered. The major concerns of the examining team were the following:
- In (f) many students wrote down the expected values table (from the GDC) and highlighted the correct expected value, 12.6. As this is a "show that" question the use of the GDC is not expected and therefore no marks are awarded for this working. Instead it is expected the use of the formula for the expected value with the correct substitutions.
- In (e) surprisingly many candidates found the \(\chi _{calc}^2\) through the use of the formula. Unfortunately this led to some incorrect answers and also to a bad use of time. The question clearly says "use your graphic display calculator" and it is worth 2 marks therefore a student should not spend more than 2 minutes to answer this part question. Time management is essential in this type of examinations and the IB rule is one minute – one mark.
In general this part question was well answered. The major concerns of the examining team were the following:
- In (f) many students wrote down the expected values table (from the GDC) and highlighted the correct expected value, 12.6. As this is a "show that" question the use of the GDC is not expected and therefore no marks are awarded for this working. Instead it is expected the use of the formula for the expected value with the correct substitutions.
- In (e) surprisingly many candidates found the \(\chi _{calc}^2\) through the use of the formula. Unfortunately this led to some incorrect answers and also to a bad use of time. The question clearly says "use your graphic display calculator" and it is worth 2 marks therefore a student should not spend more than 2 minutes to answer this part question. Time management is essential in this type of examinations and the IB rule is one minute – one mark.
In general this part question was well answered. The major concerns of the examining team were the following:
- In (f) many students wrote down the expected values table (from the GDC) and highlighted the correct expected value, 12.6. As this is a "show that" question the use of the GDC is not expected and therefore no marks are awarded for this working. Instead it is expected the use of the formula for the expected value with the correct substitutions.
- In (e) surprisingly many candidates found the \(\chi _{calc}^2\) through the use of the formula. Unfortunately this led to some incorrect answers and also to a bad use of time. The question clearly says "use your graphic display calculator" and it is worth 2 marks therefore a student should not spend more than 2 minutes to answer this part question. Time management is essential in this type of examinations and the IB rule is one minute – one mark.
In general this part question was well answered. The major concerns of the examining team were the following:
- In (f) many students wrote down the expected values table (from the GDC) and highlighted the correct expected value, 12.6. As this is a "show that" question the use of the GDC is not expected and therefore no marks are awarded for this working. Instead it is expected the use of the formula for the expected value with the correct substitutions.
- In (e) surprisingly many candidates found the \(\chi _{calc}^2\) through the use of the formula. Unfortunately this led to some incorrect answers and also to a bad use of time. The question clearly says "use your graphic display calculator" and it is worth 2 marks therefore a student should not spend more than 2 minutes to answer this part question. Time management is essential in this type of examinations and the IB rule is one minute – one mark.
In general this part question was well answered. The major concerns of the examining team were the following:
- In (f) many students wrote down the expected values table (from the GDC) and highlighted the correct expected value, 12.6. As this is a "show that" question the use of the GDC is not expected and therefore no marks are awarded for this working. Instead it is expected the use of the formula for the expected value with the correct substitutions.
- In (e) surprisingly many candidates found the \(\chi _{calc}^2\) through the use of the formula. Unfortunately this led to some incorrect answers and also to a bad use of time. The question clearly says "use your graphic display calculator" and it is worth 2 marks therefore a student should not spend more than 2 minutes to answer this part question. Time management is essential in this type of examinations and the IB rule is one minute – one mark.
In general this part question was well answered. The major concerns of the examining team were the following:
- In (f) many students wrote down the expected values table (from the GDC) and highlighted the correct expected value, 12.6. As this is a "show that" question the use of the GDC is not expected and therefore no marks are awarded for this working. Instead it is expected the use of the formula for the expected value with the correct substitutions.
- In (e) surprisingly many candidates found the \(\chi _{calc}^2\) through the use of the formula. Unfortunately this led to some incorrect answers and also to a bad use of time. The question clearly says "use your graphic display calculator" and it is worth 2 marks therefore a student should not spend more than 2 minutes to answer this part question. Time management is essential in this type of examinations and the IB rule is one minute – one mark.
Sharon and Lisa share a flat. Sharon cooks dinner three nights out of ten. If Sharon does not cook dinner, then Lisa does. If Sharon cooks dinner the probability that they have pasta is 0.75. If Lisa cooks dinner the probability that they have pasta is 0.12.
A survey was carried out in a year 12 class. The pupils were asked which pop groups they like out of the Rockers (R), the Salseros (S), and the Bluers (B). The results are shown in the following diagram.
Copy and complete the tree diagram to represent this information.
Find the probability that Lisa cooks dinner and they do not have pasta.
Find the probability that they do not have pasta.
Given that they do not have pasta, find the probability that Lisa cooked dinner.
Write down \(n(R \cap S \cap B)\).
Find \(n(R')\).
Describe which groups the pupils in the set \(S \cap B\) like.
Use set notation to describe the group of pupils who like the Rockers and the Bluers but do not like the Salseros.
There are 33 pupils in the class.
Find x.
There are 33 pupils in the class.
Find the number of pupils who like the Rockers.
Markscheme
Note: Award (A1) for each correct pair. (A3)
[3 marks]
\(0.7 \times 0.88 = 0.616{\text{ }}\left( {\frac{{77}}{{125}},{\text{ }}61.6{\text{ }}\% } \right)\) (M1)(A1)(ft)(G2)
Note: Award (M1) for multiplying the correct probabilities.
[2 marks]
\(0.3 \times 0.25 + 0.7 \times 0.88\) (M1)(M1)
Notes: Award (M1) for a relevant two-factor product, could be \(S \times NP\) OR \(L \times NP\).
Award (M1) for summing 2 two-factor products.
\({\text{P}} = 0.691{\text{ }}\left( {\frac{{691}}{{1000}},{\text{ }}69.1{\text{ }}\% } \right)\) (A1)(ft)(G2)
Notes: (ft) from their answer to (b).
[3 marks]
\(\frac{{0.616}}{{0.691}}\) (M1)(A1)
Note: Award (M1) for substituted conditional probability formula, (A1) for correct substitution.
\({\text{P}} = 0.891{\text{ }}\left( {\frac{{616}}{{691}},{\text{ }}89.1{\text{ }}\% } \right)\) (A1)(ft)(G2)
[3 marks]
3 (A1)
[1 mark]
For 5, 4, 7 (0) seen with no extra values (A1)
16 (A1)(G2)
[2 marks]
They like (both) the Salseros (S) and they like the Bluers (B) (A1)(A1)
Note: Award (A1) for “and”, (A1) for the correct groups.
[2 marks]
\(R \cap B \cap S'\) (A1)(A1)
Note: Award (A1) for \(R \cap B\), (A1) for \( \cap S'\)
[2 marks]
\(21+ 3x = 33\) (M1)
\(x = 4\) (A1)(G2)
[2 marks]
17 (A1)(ft)
[1 mark]
Examiners report
The tree diagram was quite well answered by many students, but sometimes it was missing on many papers. It seemed they had it on their examination paper because the subsequent questions were answered accurately. Conditional probability was of great difficulty to many candidates.
The tree diagram was quite well answered by many students, but sometimes it was missing on many papers. It seemed they had it on their examination paper because the subsequent questions were answered accurately. Conditional probability was of great difficulty to many candidates.
The tree diagram was quite well answered by many students, but sometimes it was missing on many papers. It seemed they had it on their examination paper because the subsequent questions were answered accurately. Conditional probability was of great difficulty to many candidates.
The tree diagram was quite well answered by many students, but sometimes it was missing on many papers. It seemed they had it on their examination paper because the subsequent questions were answered accurately. Conditional probability was of great difficulty to many candidates.
This question was well handled although part (d) proved too difficult for many candidates and demonstrated, overall, a poor level of understanding of basic set notation. Students generally had the algebraic skills required to solve for x in part (e)(ii).
This question was well handled although part (d) proved too difficult for many candidates and demonstrated, overall, a poor level of understanding of basic set notation. Students generally had the algebraic skills required to solve for x in part (e)(ii).
This question was well handled although part (d) proved too difficult for many candidates and demonstrated, overall, a poor level of understanding of basic set notation. Students generally had the algebraic skills required to solve for x in part (e)(ii).
This question was well handled although part (d) proved too difficult for many candidates and demonstrated, overall, a poor level of understanding of basic set notation. Students generally had the algebraic skills required to solve for x in part (e)(ii).
This question was well handled although part (d) proved too difficult for many candidates and demonstrated, overall, a poor level of understanding of basic set notation. Students generally had the algebraic skills required to solve for x in part (e)(ii).
This question was well handled although part (d) proved too difficult for many candidates and demonstrated, overall, a poor level of understanding of basic set notation. Students generally had the algebraic skills required to solve for x in part (e)(ii).
The seniors from Gulf High School are required to participate in exactly one after-school sport. Data were gathered from a sample of 120 students regarding their choice of sport. The following data were recorded.
A \({\chi ^2}\) test was carried out at the 5 % significance level to analyse the relationship between gender and choice of after-school sport.
Write down the null hypothesis, H0, for this test.
Find the expected value of female footballers.
Write down the number of degrees of freedom.
Write down the critical value of \(\chi ^2\), at the 5 % level of significance.
Use your graphic display calculator to determine the \(\chi _{calc}^2\) value.
Determine whether H0 should be accepted. Justify your answer.
One student is chosen at random from the 120 students.
Find the probability that this student
(i) is male;
(ii) plays tennis.
Two students are chosen at random from the 120 students.
Find the probability that
(i) both play football;
(ii) neither play basketball.
Markscheme
H0 : Gender and choice of afterschool sport are independent. (A1)
Note: Accept “not associated”, do not accept “not related”, “not correlated”, or “not linked”. Accept “the relation between gender and sport is independent”.
[1 mark]
\(\frac{{85}}{{120}} \times \frac{{48}}{{120}} \times 120\left( {\frac{{85 \times 48}}{{120}}} \right)\) (M1)
Note: Award (M1) for correct expression.
= 34 (A1)(G2)
[2 marks]
2 (A1)
[1 mark]
5.99 (5.991) (A1)(ft)
Note: Follow through from part (c).
[1 mark]
2.42 (2.42094…) (G2)
[2 marks]
Since 2.42 < 5.99 therefore accept (do not reject) H0 (R1)(A1)(ft)
Note: The numerical values need not be seen, but must be consistent with their parts (d) and (e).
OR
p-value 0.298 > 0.05 therefore accept (do not reject) H0 (R1)(A1)
Note: p-value comparison may not be used as part of a follow through solution. Do not award (A1)(R0). Follow through from parts (c), (d) and (e).
[2 marks]
(i) \(\frac{{35}}{{120}}\left( {\frac{7}{{24}},{\text{ }}0.292,{\text{ }}29.2\% } \right)\) (0.291666...) (A1)
(ii) \(\frac{{25}}{{120}}\left( {\frac{5}{{24}},{\text{ }}0.208,{\text{ }}20.8\% } \right)\) (0.208333...) (A1)
[2 marks]
(i) \(\frac{{48}}{{120}} \times \frac{{47}}{{119}}\) (A1)(M1)
Note: Award (A1) for two correct fractions, (M1) for multiplying their two fractions.
\( = \frac{{94}}{{595}}(0.158,{\text{ }}15.8\% )\) (0.157983...) (A1)(G2)
(ii) \(\frac{{73}}{{120}} \times \frac{{72}}{{119}}\) (M1)
Note: Award (M1) for multiplying correct fractions. If sampling with replacement has been used in both parts (h)(i) and (h)(ii) do not penalise in part (h)(ii). Award a maximum of (M1)(A1)(ft).
\( = \frac{{219}}{{595}}(0.368,{\text{ }}36.8\% )\) (0.368067...) (A1)(G2)
[5 marks]
Examiners report
This question was successfully attempted by the great majority. However, the test is for the mathematical independence of the two variables; it does not address “correlation” or whether there is “no relation” between them. Further, the result of the test should be determined by the comparison of the numerical values of either the chi-squared calculated and critical values or the associated p-value and the significance level of the test. The creeping use of k as the critical value is the notation used in one text book; it is not standard notation and its use is not accepted. Comments were made on the G2 forms as to whether the the null hypothesis should be “accepted” or not rejected; both forms are acceptable.
In the compound probability questions, the lack of an explicit tree diagram determined that many candidates were not able to proceed. Determining an appropriate technique is a skill that should be taught.
This question was successfully attempted by the great majority. However, the test is for the mathematical independence of the two variables; it does not address “correlation” or whether there is “no relation” between them. Further, the result of the test should be determined by the comparison of the numerical values of either the chi-squared calculated and critical values or the associated p-value and the significance level of the test. The creeping use of k as the critical value is the notation used in one text book; it is not standard notation and its use is not accepted. Comments were made on the G2 forms as to whether the the null hypothesis should be “accepted” or not rejected; both forms are acceptable.
In the compound probability questions, the lack of an explicit tree diagram determined that many candidates were not able to proceed. Determining an appropriate technique is a skill that should be taught.
This question was successfully attempted by the great majority. However, the test is for the mathematical independence of the two variables; it does not address “correlation” or whether there is “no relation” between them. Further, the result of the test should be determined by the comparison of the numerical values of either the chi-squared calculated and critical values or the associated p-value and the significance level of the test. The creeping use of k as the critical value is the notation used in one text book; it is not standard notation and its use is not accepted. Comments were made on the G2 forms as to whether the the null hypothesis should be “accepted” or not rejected; both forms are acceptable.
In the compound probability questions, the lack of an explicit tree diagram determined that many candidates were not able to proceed. Determining an appropriate technique is a skill that should be taught.
This question was successfully attempted by the great majority. However, the test is for the mathematical independence of the two variables; it does not address “correlation” or whether there is “no relation” between them. Further, the result of the test should be determined by the comparison of the numerical values of either the chi-squared calculated and critical values or the associated p-value and the significance level of the test. The creeping use of k as the critical value is the notation used in one text book; it is not standard notation and its use is not accepted. Comments were made on the G2 forms as to whether the the null hypothesis should be “accepted” or not rejected; both forms are acceptable.
In the compound probability questions, the lack of an explicit tree diagram determined that many candidates were not able to proceed. Determining an appropriate technique is a skill that should be taught.
This question was successfully attempted by the great majority. However, the test is for the mathematical independence of the two variables; it does not address “correlation” or whether there is “no relation” between them. Further, the result of the test should be determined by the comparison of the numerical values of either the chi-squared calculated and critical values or the associated p-value and the significance level of the test. The creeping use of k as the critical value is the notation used in one text book; it is not standard notation and its use is not accepted. Comments were made on the G2 forms as to whether the the null hypothesis should be “accepted” or not rejected; both forms are acceptable.
In the compound probability questions, the lack of an explicit tree diagram determined that many candidates were not able to proceed. Determining an appropriate technique is a skill that should be taught.
This question was successfully attempted by the great majority. However, the test is for the mathematical independence of the two variables; it does not address “correlation” or whether there is “no relation” between them. Further, the result of the test should be determined by the comparison of the numerical values of either the chi-squared calculated and critical values or the associated p-value and the significance level of the test. The creeping use of k as the critical value is the notation used in one text book; it is not standard notation and its use is not accepted. Comments were made on the G2 forms as to whether the the null hypothesis should be “accepted” or not rejected; both forms are acceptable.
In the compound probability questions, the lack of an explicit tree diagram determined that many candidates were not able to proceed. Determining an appropriate technique is a skill that should be taught.
This question was successfully attempted by the great majority. However, the test is for the mathematical independence of the two variables; it does not address “correlation” or whether there is “no relation” between them. Further, the result of the test should be determined by the comparison of the numerical values of either the chi-squared calculated and critical values or the associated p-value and the significance level of the test. The creeping use of k as the critical value is the notation used in one text book; it is not standard notation and its use is not accepted. Comments were made on the G2 forms as to whether the the null hypothesis should be “accepted” or not rejected; both forms are acceptable.
In the compound probability questions, the lack of an explicit tree diagram determined that many candidates were not able to proceed. Determining an appropriate technique is a skill that should be taught.
This question was successfully attempted by the great majority. However, the test is for the mathematical independence of the two variables; it does not address “correlation” or whether there is “no relation” between them. Further, the result of the test should be determined by the comparison of the numerical values of either the chi-squared calculated and critical values or the associated p-value and the significance level of the test. The creeping use of k as the critical value is the notation used in one text book; it is not standard notation and its use is not accepted. Comments were made on the G2 forms as to whether the the null hypothesis should be “accepted” or not rejected; both forms are acceptable.
In the compound probability questions, the lack of an explicit tree diagram determined that many candidates were not able to proceed. Determining an appropriate technique is a skill that should be taught.
A group of 100 customers in a restaurant are asked which fruits they like from a choice of mangoes, bananas and kiwi fruits. The results are as follows.
15 like all three fruits
22 like mangoes and bananas
33 like mangoes and kiwi fruits
27 like bananas and kiwi fruits
8 like none of these three fruits
\(x\) like only mangoes
Copy the following Venn diagram and correctly insert all values from the above information.
The number of customers that like only mangoes is equal to the number of customers that like only kiwi fruits. This number is half of the number of customers that like only bananas.
Complete your Venn diagram from part (a) with this additional information in terms of \(x\).
The number of customers that like only mangoes is equal to the number of customers that like only kiwi fruits. This number is half of the number of customers that like only bananas.
Find the value of \(x\).
The number of customers that like only mangoes is equal to the number of customers that like only kiwi fruits. This number is half of the number of customers that like only bananas.
Write down the number of customers who like
(i) mangoes;
(ii) mangoes or bananas.
The number of customers that like only mangoes is equal to the number of customers that like only kiwi fruits. This number is half of the number of customers that like only bananas.
A customer is chosen at random from the 100 customers. Find the probability that this customer
(i) likes none of the three fruits;
(ii) likes only two of the fruits;
(iii) likes all three fruits given that the customer likes mangoes and bananas.
The number of customers that like only mangoes is equal to the number of customers that like only kiwi fruits. This number is half of the number of customers that like only bananas.
Two customers are chosen at random from the 100 customers. Find the probability that the two customers like none of the three fruits.
Markscheme
(A1)(A1)(A1)
Notes: Award (A1) for 15 in the correct place.
Award (A1) for 7, 18 and 12 seen in the correct places.
Award (A1) for 8 in the correct place.
Award at most (A0)(A1)(A1) if diagram is missing the rectangle.
(A1)(A1)
Notes: Award (A1) for \(x\) seen in the correct places.
Award (A1) for \(2x\) seen in the correct place.
Award (A0)(A1)(ft) if \(x\) and \(2x\) are replaced by 10 and 20 respectively.
\(2x + x + x + 15 + 8 + 7 + 18 + 12 = 100\;\;\;(4x + 60 = 100{\text{ or equivalent)}}\) (M1)
Note: Award (M1) for equating the sum of the elements of their Venn diagram to \(100\). Equating to \(100\) may be implied.
\((x = ){\text{ }}10\) (A1)(ft)(G2)
Note: Follow through from their Venn diagram. The answer must be a positive integer.
(i) \(50\) (A1)(ft)
(ii) \(82\) (A1)(ft)
Note: Follow through from their answer to part (c) and their Venn diagram.
Award (A0)(ft)(A1)(ft) if answer is \(\frac{{50}}{{100}}\) and \(\frac{{82}}{{100}}\).
(i) \(\frac{8}{{100}}\;\;\;\left( {\frac{2}{{25}};{\text{ }}0.08;{\text{ }}8\% } \right)\) (A1)
Note: Correct answer only. There is no follow through.
(ii) \(\frac{{37}}{{100}}\;\;\;(0.37,{\text{ }}37\% )\) (A1)(ft)
Note: Follow through from their Venn diagram.
(iii) \(\frac{{15}}{{22}}\;\;\;(0.681;{\text{ }}0.682;{\text{ }}68.2\% )\;\;\;(0.681818 \ldots )\) (A1)(A1)(ft)(G2)
Notes: Award (A1) for numerator, (A1)(ft) for denominator, follow through from their Venn diagram. Award (A0)(A0) if answer is given as incorrect reduced fraction without working.
\(\frac{8}{{100}} \times \frac{7}{{99}}\) (A1)(ft)(M1)
Note: Award (A1)(ft) for correct fractions, follow through from their answer to part (e)(i), (M1) for multiplying their fractions.
\( = \frac{{56}}{{9900}}\;\;\;\left( {\frac{{14}}{{2477}},{\text{ }}0.00565656 \ldots ,{\text{ }}0.00566,{\text{ }}0.0056,{\text{ }}0.566\% } \right)\) (A1)(ft)(G2)
Examiners report
Neil has three dogs. Two are brown and one is grey. When he feeds the dogs, Neil uses three bowls and gives them out randomly. There are two red bowls and one yellow bowl. This information is shown on the tree diagram below.
There are 49 mice in a pet shop.
30 mice are white.
27 mice are male.
18 mice have short tails.
8 mice are white and have short tails.
11 mice are male and have short tails.
7 mice are male but neither white nor short-tailed.
5 mice have all three characteristics and
2 have none.
Copy the diagram below to your examination script.
One of the dogs is chosen at random.
(i) Find P (the dog is grey and has the yellow bowl).
(ii) Find P (the dog does not get the yellow bowl).
Neil often takes the dogs to the park after they have eaten. He has noticed that the grey dog plays with a stick for a quarter of the time and both brown dogs play with sticks for half of the time. This information is shown on the tree diagram below.
(i) Copy the tree diagram and add the four missing probability values on the branches that refer to playing with a stick.
During a trip to the park, one of the dogs is chosen at random.
(ii) Find P (the dog is grey or is playing with a stick, but not both).
(iii) Find P (the dog is grey given that the dog is playing with a stick).
(iv) Find P (the dog is grey and was fed from the yellow bowl and is not playing with a stick).
Complete the diagram, using the information given in the question.
Find (i) \(n(M \cap W)\)
(ii) \(n(M′ \cup S)\)
Two mice are chosen without replacement.
Find P (both mice are short-tailed).
Markscheme
(i) P (a dog is grey and has the yellow bowl)
\( = \frac{1}{3} \times \frac{1}{3} = \frac{1}{9}( = 0.111)\) (M1)(A1)(G2)
The (M1) is for multiplying two values along any branch of the tree.
(ii) P (dog does not get yellow bowl) \( = \frac{2}{3}\) ( = 0.667 (3sf) or 0.6) (A1)
[3 marks]
(i) The tree diagram should show the values \(\frac{1}{2},\frac{1}{2}\) for the brown branch and \(\frac{1}{4},\frac{3}{4}\) in the correct positions for the grey branch. (A1)(A1)(ft)
Follow through if the branches are interchanged.
(ii) P (the dog is grey or is playing with a stick, but not both)
\( = \frac{1}{3} \times \frac{3}{4} + \frac{2}{3} \times \frac{1}{2}\) (M1)
\( = \frac{7}{{12}}\) ( = 0.583) (A1)(ft)(G1)
The (M1) is for showing two correct products (whether added or not). Follow through from b(i). Award (M1) for \( \frac{1}{3} + \frac{1}{4}\) (must be a sum).
(iii) P (dog is grey given that it is playing with stick)
\(\frac{{P(G \cap S)}}{{P(S)}} = \frac{{\frac{1}{3} \times \frac{1}{4}}}{{\left( {\frac{2}{3} \times \frac{1}{2}} \right) + \left( {\frac{1}{3} \times \frac{1}{4}} \right)}}\) or \(\frac{1}{{12}}/\frac{5}{{12}}\) (M1)(A1)(ft)
(M1) for substituted conditional probability formula, (A1) for correct substitutions.
\( = \frac{1}{5}\) ( = 0.2) (A1)(ft)(G2)
(iv) P (grey and fed from yellow bowl and not playing with stick) \( = \frac{1}{3} \times \frac{1}{3} \times \frac{3}{4} = \frac{1}{{12}}\) ( = \(\frac{3}{{36}}\) = 0.0833 3sf). (M1)(A1)(ft)(G1)
(M1) is for product of 3 reasonable probability values.
[9 marks]
(A1)(A1)(A1)(ft)(A1)(ft)
Award (A1) for 2 (must be in a box), (A1) for 7, (A1)(ft) for 6 and 4, (A1)(ft) for 9 and 13. Observe the assignment of (ft) marks strictly here. Example A common error is likely to be 11 instead of 6 (A0). In this case follow through to 4 and 18 (A1)(ft) for the final pair. Here the 4 follows from the total of 27 for n(M).
[4 marks]
(i) \(n(M \cap W) = 14\) (A1)(ft)
(ii) \(n(M' \cup S) = 22 + 11\) OR \(15 + 18\) (A1)(ft)
= 33 (A1)(ft)
Award (A2) if answer 33 is seen. Award (A1) for any of 22, 11, 15 or 18 seen but 33 absent.
[3 marks]
P (both mice short-tailed) \( = \frac{{18}}{{49}} \times \frac{{17}}{{48}} = \frac{{306}}{{352}}\) (= 0.130). (M1)(A1)(ft)(G1)
(Allow alternatives such as 153/1176 or 51/392.) Award (M1) for any of \(\frac{{18}}{{49}}\) and \(\frac{{17}}{{48}}\) or \(\frac{{18}}{{49}} \times \frac{{17}}{{49}}\) or \(\frac{{18}}{{49}} + \frac{{17}}{{48}}\) seen.
[2 marks]
Examiners report
(i) (a),(b) Elementary probability calculations were performed well and compound ones often poorly. Filling in of the tree diagram in b(i) was quite well done. Conditional probability in particular was poorly implemented.
(i) (a),(b) Elementary probability calculations were performed well and compound ones often poorly. Filling in of the tree diagram in b(i) was quite well done. Conditional probability in particular was poorly implemented.
(ii) Most candidates had some idea how to fill in the numbers on the diagram. Full marks were common here and most candidates got some of the marks.
Part b(i) was handled better than b(ii), with the complement causing problems. Extensive follow-through was used here from (a).
Part (c) was rarely completed, perhaps due to time constraints, but also due to lack of understanding.
On one day 180 flights arrived at a particular airport. The distance travelled and the arrival status for each incoming flight was recorded. The flight was then classified as on time, slightly delayed, or heavily delayed.
The results are shown in the following table.
A χ2 test is carried out at the 10 % significance level to determine whether the arrival status of incoming flights is independent of the distance travelled.
The critical value for this test is 7.779.
A flight is chosen at random from the 180 recorded flights.
State the alternative hypothesis.
Calculate the expected frequency of flights travelling at most 500 km and arriving slightly delayed.
Write down the number of degrees of freedom.
Write down the χ2 statistic.
Write down the associated p-value.
State, with a reason, whether you would reject the null hypothesis.
Write down the probability that this flight arrived on time.
Given that this flight was not heavily delayed, find the probability that it travelled between 500 km and 5000 km.
Two flights are chosen at random from those which were slightly delayed.
Find the probability that each of these flights travelled at least 5000 km.
Markscheme
The arrival status is dependent on the distance travelled by the incoming flight (A1)
Note: Accept “associated” or “not independent”.
[1 mark]
\(\frac{{60 \times 45}}{{180}}\) OR \(\frac{{60}}{{180}} \times \frac{{45}}{{180}} \times 180\) (M1)
Note: Award (M1) for correct substitution into expected value formula.
= 15 (A1) (G2)
[2 marks]
4 (A1)
Note: Award (A0) if “2 + 2 = 4” is seen.
[1 mark]
9.55 (9.54671…) (G2)
Note: Award (G1) for an answer of 9.54.
[2 marks]
0.0488 (0.0487961…) (G1)
[1 mark]
Reject the Null Hypothesis (A1)(ft)
Note: Follow through from their hypothesis in part (a).
9.55 (9.54671…) > 7.779 (R1)(ft)
OR
0.0488 (0.0487961…) < 0.1 (R1)(ft)
Note: Do not award (A1)(ft)(R0)(ft). Follow through from part (d). Award (R1)(ft) for a correct comparison, (A1)(ft) for a consistent conclusion with the answers to parts (a) and (d). Award (R1)(ft) for χ2calc > χ2crit , provided the calculated value is explicitly seen in part (d)(i).
[2 marks]
\(\frac{{52}}{{180}}\,\,\left( {0.289,\,\,\frac{{13}}{{45}},\,\,28.9\,{\text{% }}} \right)\) (A1)(A1) (G2)
Note: Award (A1) for correct numerator, (A1) for correct denominator.
[2 marks]
\(\frac{{35}}{{97}}\,\,\left( {0.361,\,\,36.1\,{\text{% }}} \right)\) (A1)(A1) (G2)
Note: Award (A1) for correct numerator, (A1) for correct denominator.
[2 marks]
\(\frac{{14}}{{45}} \times \frac{{13}}{{44}}\) (A1)(M1)
Note: Award (A1) for two correct fractions and (M1) for multiplying their two fractions.
\( = \frac{{182}}{{1980}}\,\,\left( {0.0919,\,\,\frac{{91}}{{990}},\,0.091919 \ldots ,\,9.19\,{\text{% }}} \right)\) (A1) (G2)
[3 marks]
Examiners report
A survey of \(400\) people is carried out by a market research organization in two different cities, Buenos Aires and Montevideo. The people are asked which brand of cereal they prefer out of Chocos, Zucos or Fruti. The table below summarizes their responses.
The following table shows the cost in \({\text{AUD}}\) of seven paperback books chosen at random, together with the number of pages in each book.
One person is chosen at random from those surveyed. Find the probability that this person
(i) does not prefer Zucos;
(ii) prefers Chocos, given that they live in Montevideo.
Two people are chosen at random from those surveyed. Find the probability that they both prefer Fruti.
The market research organization tests the survey data to determine whether the brand of cereal preferred is associated with a city. A chi-squared test at the \(5\% \) level of significance is performed.
State the null hypothesis.
The market research organization tests the survey data to determine whether the brand of cereal preferred is associated with a city. A chi-squared test at the \(5\% \) level of significance is performed.
State the number of degrees of freedom.
The market research organization tests the survey data to determine whether the brand of cereal preferred is associated with a city. A chi-squared test at the \(5\% \) level of significance is performed.
Show that the expected frequency for the number of people who live in Montevideo and prefer Zucos is \(63\).
The market research organization tests the survey data to determine whether the brand of cereal preferred is associated with a city. A chi-squared test at the \(5\% \) level of significance is performed.
Write down the chi-squared statistic for this data.
The market research organization tests the survey data to determine whether the brand of cereal preferred is associated with a city. A chi-squared test at the \(5\% \) level of significance is performed.
State whether the market research organization would accept the null hypothesis. Clearly justify your answer.
Plot these pairs of values on a scatter diagram. Use a scale of \(1{\text{ cm}}\) to represent \(50\) pages on the horizontal axis and \(1{\text{ cm}}\) to represent \(1{\text{ AUD}}\) on the vertical axis.
Write down the linear correlation coefficient, \(r\), for the data.
Stephen wishes to buy a paperback book which has \(350\) pages in it. He plans to draw a line of best fit to determine the price. State whether or not this is an appropriate method in this case and justify your answer.
Markscheme
(i) \(\frac{{280}}{{400}}{\text{ }}(0.7{\text{, }}70\% {\text{ or equivalent}})\) (A1)(A1)(G2)
Note: (A1) for correct numerator, (A1) for correct denominator.
(ii) \(\frac{{57}}{{210}}{\text{ }}\left( {\frac{{19}}{{70}}{\text{, }}0.271{\text{, }}27.1\% } \right)\) (A1)(A1)(G2)
Note: (A1) for correct numerator, (A1) for correct denominator.
[4 marks]
\(\frac{{180}}{{400}} \times \frac{{179}}{{399}}\) (A1)(M1)
Note: (A1) for correct values seen, (M1) for multiplying their two values, (A1) for correct answer.
\( = \frac{{537}}{{2660}}{\text{ }}( = 0.202)\) (A1)(G3)
[3 marks]
\({{\text{H}}_0}\) : ‘the preference of brand of cereal is independent of the city’. (A1)
OR
\({{\text{H}}_0}\) : ‘there is no association between the brand of cereal and city’.
[1 mark]
\(df = 2\) (A1)
[1 mark]
\(\frac{{210 \times 120}}{{400}}\) (M1)(A1)
Note: (M1) for substituting in correct formula, (A1) for correct values.
\( = 63\) (AG)
Note: Final line must be seen or previous (A1) mark is lost.
[2 marks]
\(39.3\) (G2)
Note: Award (G1)(A0)(AP) if answers not to 3 significant figures.
[2 marks]
\(p - {\text{value}} < 0.05\) (R1)(ft)
Do not accept \({{{\text{H}}_0}}\) . (A1)(ft)
Notes: Allow ‘Reject \({{{\text{H}}_0}}\) or equivalent’. (ft) from their \({\chi ^2}\) statistic.
Award (R1)(ft) for comparing the appropriate values. (A1)(ft) can be awarded only if the conclusion is valid according to the comparison given. If no reason given or if reason is wrong both marks are lost. Note that (R1)(A0)(ft) can be awarded but (R0)(A1)(ft) cannot.
[2 marks]
(A1)(A1)(A1)
Notes: (A1) for label and scales, (A2) for all points correct, (A1) for 5 or 6 correct. Award a maximum of (A2) if points are joined.
[3 marks]
\(r = - 0.141\) (G2)
Note: If negative sign is missing award (G1)(G0).
[2 marks]
‘The coefficient of correlation is too low, (very) weak (linear) relationship’. (R1)
Not a sensible thing to do, accept ‘no’. (A1)
Note: Do not award (R0)(A1). The correlation coefficient has to be mentioned in their reasoning.
[2 marks]
Examiners report
Candidates answered part (a) correctly. Some lost one out of the 4 marks for making an error in the denominator of the conditional probability. In (b) many students failed to see that (b) was 'without replacement'. Parts (c), (d) and (e) seemed to be very well done by some centres and uniformly badly by others. In (e) many gave the table from the GDC and highlighted the value 63 for which no mark was gained. Expected value formula should have been used instead.
Candidates answered part (a) correctly. Some lost one out of the 4 marks for making an error in the denominator of the conditional probability. In (b) many students failed to see that (b) was 'without replacement'. Parts (c), (d) and (e) seemed to be very well done by some centres and uniformly badly by others. In (e) many gave the table from the GDC and highlighted the value 63 for which no mark was gained. Expected value formula should have been used instead.
Candidates answered part (a) correctly. Some lost one out of the 4 marks for making an error in the denominator of the conditional probability. In (b) many students failed to see that (b) was 'without replacement'. Parts (c), (d) and (e) seemed to be very well done by some centres and uniformly badly by others. In (e) many gave the table from the GDC and highlighted the value 63 for which no mark was gained. Expected value formula should have been used instead.
Candidates answered part (a) correctly. Some lost one out of the 4 marks for making an error in the denominator of the conditional probability. In (b) many students failed to see that (b) was 'without replacement'. Parts (c), (d) and (e) seemed to be very well done by some centres and uniformly badly by others. In (e) many gave the table from the GDC and highlighted the value 63 for which no mark was gained. Expected value formula should have been used instead.
Candidates answered part (a) correctly. Some lost one out of the 4 marks for making an error in the denominator of the conditional probability. In (b) many students failed to see that (b) was 'without replacement'. Parts (c), (d) and (e) seemed to be very well done by some centres and uniformly badly by others. In (e) many gave the table from the GDC and highlighted the value 63 for which no mark was gained. Expected value formula should have been used instead.
Candidates answered part (a) correctly. Some lost one out of the 4 marks for making an error in the denominator of the conditional probability. In (b) many students failed to see that (b) was 'without replacement'. Parts (c), (d) and (e) seemed to be very well done by some centres and uniformly badly by others. In (e) many gave the table from the GDC and highlighted the value 63 for which no mark was gained. Expected value formula should have been used instead.
Candidates answered part (a) correctly. Some lost one out of the 4 marks for making an error in the denominator of the conditional probability. In (b) many students failed to see that (b) was 'without replacement'. Parts (c), (d) and (e) seemed to be very well done by some centres and uniformly badly by others. In (e) many gave the table from the GDC and highlighted the value 63 for which no mark was gained. Expected value formula should have been used instead.
The graph was well done with almost all candidates labelling and scaling the axes correctly. A minority of students joined the points or drew the graph on lined paper which prevented them from gaining full marks in this part of the question.
In (b) some candidates were not able to calculate the linear correlation coefficient. A few G2 comments pointed out that the command term used may have been ambiguous to some candidates and they did not think that they could use their GDC to find r. Some attempted to use the formula even though the value of \({S_{xy}}\) was not given. The guide says that 'A GDC can be used to calculate r when raw data is given'. This potential unfairness was taken into consideration during the setting of boundaries so that no candidate was disadvantaged by the possible ambiguous wording of the question. In future the command term 'Using your GDC' or 'Write down' will be used in similar questions.
Some students who did use the GDC gave \({r^2}\) instead of \(r\). This really caught the attention of many examiners as \({r^2}\) is not in the syllabus.
The graph was well done with almost all candidates labelling and scaling the axes correctly. A minority of students joined the points or drew the graph on lined paper which prevented them from gaining full marks in this part of the question.
In (b) some candidates were not able to calculate the linear correlation coefficient. A few G2 comments pointed out that the command term used may have been ambiguous to some candidates and they did not think that they could use their GDC to find r. Some attempted to use the formula even though the value of \({S_{xy}}\) was not given. The guide says that 'A GDC can be used to calculate r when raw data is given'. This potential unfairness was taken into consideration during the setting of boundaries so that no candidate was disadvantaged by the possible ambiguous wording of the question. In future the command term 'Using your GDC' or 'Write down' will be used in similar questions.
Some students who did use the GDC gave \({r^2}\) instead of \(r\). This really caught the attention of many examiners as \({r^2}\) is not in the syllabus.
The graph was well done with almost all candidates labelling and scaling the axes correctly. A minority of students joined the points or drew the graph on lined paper which prevented them from gaining full marks in this part of the question.
In (b) some candidates were not able to calculate the linear correlation coefficient. A few G2 comments pointed out that the command term used may have been ambiguous to some candidates and they did not think that they could use their GDC to find r. Some attempted to use the formula even though the value of \({S_{xy}}\) was not given. The guide says that 'A GDC can be used to calculate r when raw data is given'. This potential unfairness was taken into consideration during the setting of boundaries so that no candidate was disadvantaged by the possible ambiguous wording of the question. In future the command term 'Using your GDC' or 'Write down' will be used in similar questions.
Some students who did use the GDC gave \({r^2}\) instead of \(r\). This really caught the attention of many examiners as \({r^2}\) is not in the syllabus.
\(180\) people were interviewed and asked what types of transport they had used in the last year from a choice of airplane \((A)\), train \((T)\) or bus \((B)\). The following information was obtained.
\(47\) had travelled by airplane
\(68\) had travelled by train
\(122\) had travelled by bus
\(25\) had travelled by airplane and train
\(32\) had travelled by airplane and bus
\(35\) had travelled by train and bus
\(20\) had travelled by all three types of transport
Draw a Venn diagram to show the above information.
Find the number of people who, in the last year, had travelled by
(i) bus only;
(ii) both airplane and bus but not by train;
(iii) at least two types of transport;
(iv) none of the three types of transport.
A person is selected at random from those who were interviewed.
Find the probability that the person had used only one type of transport in the last year.
Given that the person had used only one type of transport in the last year, find the probability that the person had travelled by airplane.
Markscheme
(A1)(A1)(A1)(A1)
Note: Award (A1) for a rectangle with \(3\) intersecting clearly labelled circles.
Award (A1) for \(20\) in correct region.
Award (A1) for \(15\), \(12\), \(5\) in correct regions.
Award (A1) for \(75\), \(28\), \(10\) in correct regions.
(i) \(75\) (A1)(ft)
Note: Follow through from their Venn diagram.
(ii) \(12\) (A1)(ft)
Note: Follow through from their Venn diagram.
(iii) \(15 + 20 + 12 + 5\) (M1)
\( = 52\) (A1)(ft)(G2)
Note: Award (M1) for addition of their \(15\), \(20\), \(12\) and \(5\). Follow through from their Venn diagram.
(iv) \(180 - 165\) (M1)
Note: Award BI for their \(165\), or a sum adding to their \(165\), seen.
\(15\) (A1)(ft)(G2)
Note: Follow through from their Venn diagram.
\(\frac{{113}}{{180}}\,\,\,(0.628,\,\,62.8\,\% ,\,\,0.62777...)\) (A1)(ft)(A1)(G2)
Note: Award (A1)(ft) for correct numerator. Follow through from their Venn diagram.
Award (A1) for \(180\) in the denominator.
\(\frac{{10}}{{113}}\,\,\,(0.0885,\,\,8.85\,\% ,\,\,0.08849...)\) (A1)(ft)(A1)(ft)(G2)
Note: Award (A1)(ft) for correct numerator, (A1)(ft) for correct denominator. Follow through from their Venn diagram or numerator from part (c).
Examiners report
Question 1: Sets and probability
In part (a), a surprising number of candidates could not construct the Venn diagram correctly, based on the given information. This led to problems with the rest of the parts although they were usually awarded follow-through marks in part (b). Part (b) which required interpreting the information from their Venn diagram was generally well done. Some candidates gave the probability rather than number of people. Most candidates were successful at the simple probability but many struggled with the conditional probability.
Question 1: Sets and probability
In part (a), a surprising number of candidates could not construct the Venn diagram correctly, based on the given information. This led to problems with the rest of the parts although they were usually awarded follow-through marks in part (b). Part (b) which required interpreting the information from their Venn diagram was generally well done. Some candidates gave the probability rather than number of people. Most candidates were successful at the simple probability but many struggled with the conditional probability.
Question 1: Sets and probability
In part (a), a surprising number of candidates could not construct the Venn diagram correctly, based on the given information. This led to problems with the rest of the parts although they were usually awarded follow-through marks in part (b). Part (b) which required interpreting the information from their Venn diagram was generally well done. Some candidates gave the probability rather than number of people. Most candidates were successful at the simple probability but many struggled with the conditional probability.
Question 1: Sets and probability
In part (a), a surprising number of candidates could not construct the Venn diagram correctly, based on the given information. This led to problems with the rest of the parts although they were usually awarded follow-through marks in part (b). Part (b) which required interpreting the information from their Venn diagram was generally well done. Some candidates gave the probability rather than number of people. Most candidates were successful at the simple probability but many struggled with the conditional probability.
Contestants in a TV gameshow try to get through three walls by passing through doors without falling into a trap. Contestants choose doors at random.
If they avoid a trap they progress to the next wall.
If a contestant falls into a trap they exit the game before the next contestant plays.
Contestants are not allowed to watch each other attempt the game.
The first wall has four doors with a trap behind one door.
Ayako is a contestant.
Natsuko is the second contestant.
The second wall has five doors with a trap behind two of the doors.
The third wall has six doors with a trap behind three of the doors.
The following diagram shows the branches of a probability tree diagram for a contestant in the game.
Write down the probability that Ayako avoids the trap in this wall.
Find the probability that only one of Ayako and Natsuko falls into a trap while attempting to pass through a door in the first wall.
Copy the probability tree diagram and write down the relevant probabilities along the branches.
A contestant is chosen at random. Find the probability that this contestant fell into a trap while attempting to pass through a door in the second wall.
A contestant is chosen at random. Find the probability that this contestant fell into a trap.
120 contestants attempted this game.
Find the expected number of contestants who fell into a trap while attempting to pass through a door in the third wall.
Markscheme
\(\frac{3}{4}\) (0.75, 75%) (A1)
[1 mark]
\(\frac{3}{4} \times \frac{1}{4} + \frac{1}{4} \times \frac{3}{4}\) OR \(2 \times \frac{3}{4} \times \frac{1}{4}\) (M1)(M1)
Note: Award (M1) for their product \(\frac{1}{4} \times \frac{3}{4}\) seen, and (M1) for adding their two products or multiplying their product by 2.
\( = \frac{3}{8}\,\,\,\,\left( {\frac{6}{{16}},\,\,0.375,\,\,37.5{\text{% }}} \right)\) (A1)(ft) (G3)
Note: Follow through from part (a), but only if the sum of their two fractions is 1.
[3 marks]
(A1)(ft)(A1)(A1)
Note: Award (A1) for each correct pair of branches. Follow through from part (a).
[3 marks]
\(\frac{3}{4} \times \frac{2}{5}\) (M1)
Note: Award (M1) for correct probabilities multiplied together.
\( = \frac{3}{{10}}\,\,\,\left( {0.3,\,\,30{\text{% }}} \right)\) (A1)(ft) (G2)
Note: Follow through from their tree diagram or part (a).
[2 marks]
\(1 - \frac{3}{4} \times \frac{2}{5} \times \frac{3}{6}\) OR \(\frac{1}{4} + \frac{3}{4} \times \frac{2}{5} + \frac{3}{4} \times \frac{3}{5} \times \frac{3}{6}\) (M1)(M1)
Note: Award (M1) for \(\frac{3}{4} \times \frac{3}{5} \times \frac{3}{6}\) and (M1) for subtracting their correct probability from 1, or adding to their \(\frac{1}{4} + \frac{3}{4} \times \frac{2}{5}\).
\( = \frac{{93}}{{120}}\,\,\,\,\left( {\frac{{31}}{{40}},\,\,0.775,\,\,77.5{\text{% }}} \right)\) (A1)(ft) (G2)
Note: Follow through from their tree diagram.
[3 marks]
\(\frac{3}{4} \times \frac{3}{5} \times \frac{3}{6} \times 120\) (M1)(M1)
Note: Award (M1) for \(\frac{3}{4} \times \frac{3}{5} \times \frac{3}{6}\,\,\,\,\left( {\frac{3}{4} \times \frac{3}{5} \times \frac{3}{6}\,\,{\text{OR}}\,\,\frac{{27}}{{120}}\,\,{\text{OR}}\,\,\frac{9}{{40}}} \right)\) and (M1) for multiplying by 120.
= 27 (A1)(ft) (G3)
Note: Follow through from their tree diagram or their \(\frac{3}{4} \times \frac{3}{5} \times \frac{3}{6}\) from their calculation in part (d)(ii).
[3 marks]
Examiners report
A group of students at Dune Canyon High School were surveyed. They were asked which of the following products: books (B), music (M) or films (F), they downloaded from the internet.
The following results were obtained:
100 students downloaded music;
95 students downloaded films;
68 students downloaded films and music;
52 students downloaded books and music;
50 students downloaded films and books;
40 students downloaded all three products;
8 students downloaded books only;
25 students downloaded none of the three products.
Use the above information to complete a Venn diagram.
Calculate the number of students who were surveyed.
i) On your Venn diagram, shade the set \({\left( {F \cup M} \right) \cap B'}\) . Do not shade any labels or values on the diagram.
ii) Find \(n\left( {\left( {F \cup M} \right) \cap B'} \right)\) .
A student who was surveyed is chosen at random.
Find the probability that
(i) the student downloaded music;
(ii) the student downloaded books, given that they had not downloaded films;
(iii) the student downloaded at least two of the products.
Dune Canyon High School has 850 students.
Find the expected number of students at Dune Canyon High School that downloaded music.
Markscheme
(A1)(A1)(A1)(A1)(A1)
Note: Award (A1) for labelled sets B, M and F inside a universal set (label U is not required).
Award (A1) for \({\text{40}}\) in central area.
Award (A1) for correct \({\text{10, 12, 28}}\) in the other intersecting regions.
Award (A1) for \({\text{8, 20}}\) and \({\text{17}}\) in correct regions.
Award (A1) for correct \({\text{25}}\).
\(8 + 12 + 20 + 10 + 40 + 28 + 17 + 25\) (M1)
\( = 160\) (A1)(ft)(G2)
Note: Award (M1) for adding all values. Follow through from their Venn Diagram.
i)
(A1)
ii) \(20 + 28 + 17\) (M1)
OR
\((100 + 95 - 68) - (10 + 40 + 12)\) (M1)
\( = 65\) (A1)(ft)(G2)
Note: Award (M1) for addition of the correct values from their diagram. Follow through from part (a) or (b) and part (c)(i).
i) \(\frac{{100}}{{160}}\,\,\left( {\frac{5}{8},\,\,0.625,\,\,62.5\% } \right)\) (A1)(A1)(ft)
Note: Award (A1) for correct numerator, (A1)(ft) for correct denominator. Follow through from part (b).
ii) \(\frac{{20}}{{65}}\,\,\left( {\frac{4}{{13}},\,\,0.308,\,\,30.8\% } \right)\,\,\,(0.307692...)\) (A1)(ft)(A1)(ft)
Note: Award (A1)(ft) for correct numerator, (A1)(ft) for correct denominator. Follow through from part (a).
iii) \(\frac{{90}}{{160}}\,\,\left( {\frac{9}{{16}},\,\,0.563,\,\,56.3\% } \right)\,\,\,(0.5625)\) (A1)(ft)(A1)(ft)
Note: Award (A1)(ft) for correct numerator, (A1)(ft) for correct denominator. Follow through from parts (a) and (b).
\(\frac{{100}}{{160}} \times 850\) (M1)
Note: Award (M1) for their part (d)(i) multiplied by \(850\).
\( = 531\,\,\,(531.25)\) (A1)(ft)(G2)
Note: Follow through from part (d)(i) or from part (b).
Examiners report
Question 2: Venn diagram, probability and expected value.
Candidates were able to draw a labelled Venn diagram and correctly place 40 and 25. A common mistake was to misinterpret the intersection of sets. In most cases this resulted only in the loss of 2 marks. Many added correctly the values in their diagram and follow-through marks were awarded irrespective of working seen, allowing the candidates who produced an incorrect diagram to obtain full marks further in the question. The most common error was not including the 25 in their total. For part (c) many correct areas, but also many incorrect areas were seen. Again follow-through marks were awarded for part (c)(ii) irrespective of working shown. Some candidates just counted the number of regions. The simple probabilities in (d)(i) and (iii) were answered correctly by the majority, the conditional probability in part (d)(ii) had very often an incorrect denominator. Some candidates with an incorrect Venn diagram lost a mark in part (d)(i) as they used the value from their diagram for the numerator and not the 100 given in the question. Candidates should be aware that when values are given in the question those should always be used and follow-through marks will not be available. Many were able to find the expected number of students in part (e). Some candidates lost follow-through marks for not showing their working here.
Question 2: Venn diagram, probability and expected value.
Candidates were able to draw a labelled Venn diagram and correctly place 40 and 25. A common mistake was to misinterpret the intersection of sets. In most cases this resulted only in the loss of 2 marks. Many added correctly the values in their diagram and follow-through marks were awarded irrespective of working seen, allowing the candidates who produced an incorrect diagram to obtain full marks further in the question. The most common error was not including the 25 in their total. For part (c) many correct areas, but also many incorrect areas were seen. Again follow-through marks were awarded for part (c)(ii) irrespective of working shown. Some candidates just counted the number of regions. The simple probabilities in (d)(i) and (iii) were answered correctly by the majority, the conditional probability in part (d)(ii) had very often an incorrect denominator. Some candidates with an incorrect Venn diagram lost a mark in part (d)(i) as they used the value from their diagram for the numerator and not the 100 given in the question. Candidates should be aware that when values are given in the question those should always be used and follow-through marks will not be available. Many were able to find the expected number of students in part (e). Some candidates lost follow-through marks for not showing their working here.
Question 2: Venn diagram, probability and expected value.
Candidates were able to draw a labelled Venn diagram and correctly place 40 and 25. A common mistake was to misinterpret the intersection of sets. In most cases this resulted only in the loss of 2 marks. Many added correctly the values in their diagram and follow-through marks were awarded irrespective of working seen, allowing the candidates who produced an incorrect diagram to obtain full marks further in the question. The most common error was not including the 25 in their total. For part (c) many correct areas, but also many incorrect areas were seen. Again follow-through marks were awarded for part (c)(ii) irrespective of working shown. Some candidates just counted the number of regions. The simple probabilities in (d)(i) and (iii) were answered correctly by the majority, the conditional probability in part (d)(ii) had very often an incorrect denominator. Some candidates with an incorrect Venn diagram lost a mark in part (d)(i) as they used the value from their diagram for the numerator and not the 100 given in the question. Candidates should be aware that when values are given in the question those should always be used and follow-through marks will not be available. Many were able to find the expected number of students in part (e). Some candidates lost follow-through marks for not showing their working here.
Question 2: Venn diagram, probability and expected value.
Candidates were able to draw a labelled Venn diagram and correctly place 40 and 25. A common mistake was to misinterpret the intersection of sets. In most cases this resulted only in the loss of 2 marks. Many added correctly the values in their diagram and follow-through marks were awarded irrespective of working seen, allowing the candidates who produced an incorrect diagram to obtain full marks further in the question. The most common error was not including the 25 in their total. For part (c) many correct areas, but also many incorrect areas were seen. Again follow-through marks were awarded for part (c)(ii) irrespective of working shown. Some candidates just counted the number of regions. The simple probabilities in (d)(i) and (iii) were answered correctly by the majority, the conditional probability in part (d)(ii) had very often an incorrect denominator. Some candidates with an incorrect Venn diagram lost a mark in part (d)(i) as they used the value from their diagram for the numerator and not the 100 given in the question. Candidates should be aware that when values are given in the question those should always be used and follow-through marks will not be available. Many were able to find the expected number of students in part (e). Some candidates lost follow-through marks for not showing their working here.
Question 2: Venn diagram, probability and expected value.
Candidates were able to draw a labelled Venn diagram and correctly place 40 and 25. A common mistake was to misinterpret the intersection of sets. In most cases this resulted only in the loss of 2 marks. Many added correctly the values in their diagram and follow-through marks were awarded irrespective of working seen, allowing the candidates who produced an incorrect diagram to obtain full marks further in the question. The most common error was not including the 25 in their total. For part (c) many correct areas, but also many incorrect areas were seen. Again follow-through marks were awarded for part (c)(ii) irrespective of working shown. Some candidates just counted the number of regions. The simple probabilities in (d)(i) and (iii) were answered correctly by the majority, the conditional probability in part (d)(ii) had very often an incorrect denominator. Some candidates with an incorrect Venn diagram lost a mark in part (d)(i) as they used the value from their diagram for the numerator and not the 100 given in the question. Candidates should be aware that when values are given in the question those should always be used and follow-through marks will not be available. Many were able to find the expected number of students in part (e). Some candidates lost follow-through marks for not showing their working here.