
SL Paper 2
As part of his IB Biology field work, Barry was asked to measure the circumference of trees, in centimetres, that were growing at different distances, in metres, from a river bank. His results are summarized in the following table.

State whether distance from the river bank is a continuous or discrete variable.
On graph paper, draw a scatter diagram to show Barry’s results. Use a scale of 1 cm to represent 5 m on the x-axis and 1 cm to represent 10 cm on the y-axis.
Write down
(i) the mean distance, \(\bar x\), of the trees from the river bank;
(ii) the mean circumference, \(\bar y\), of the trees.
Plot and label the point \({\text{M}}(\bar x,{\text{ }}\bar y)\) on your graph.
Write down
(i) the Pearson’s product–moment correlation coefficient, \(r\), for Barry’s results;
(ii) the equation of the regression line \(y\) on \(x\), for Barry’s results.
Draw the regression line \(y\) on \(x\) on your graph.
Use the equation of the regression line \(y\) on \(x\) to estimate the circumference of a tree that is 40 m from the river bank.
The table below shows the distribution of test grades for 50 IB students at Greendale School.

A student is chosen at random from these 50 students.
A second student is chosen at random from these 50 students.
The number of minutes that the 50 students spent preparing for the test was normally distributed with a mean of 105 minutes and a standard deviation of 20 minutes.
Calculate the mean test grade of the students;
Calculate the standard deviation.
Find the median test grade of the students.
Find the interquartile range.
Find the probability that this student scored a grade 5 or higher.
Given that the first student chosen at random scored a grade 5 or higher, find the probability that both students scored a grade 6.
Calculate the probability that a student chosen at random spent at least 90 minutes preparing for the test.
Calculate the expected number of students that spent at least 90 minutes preparing for the test.
In the month before their IB Diploma examinations, eight male students recorded the number of hours they spent on social media.
For each student, the number of hours spent on social media (\(x\)) and the number of IB Diploma points obtained (\(y\)) are shown in the following table.

Use your graphic display calculator to find
Ten female students also recorded the number of hours they spent on social media in the month before their IB Diploma examinations. Each of these female students spent between 3 and 30 hours on social media.
The equation of the regression line y on x for these ten female students is
\[y = - \frac{2}{3}x + \frac{{125}}{3}.\]
An eleventh girl spent 34 hours on social media in the month before her IB Diploma examinations.
On graph paper, draw a scatter diagram for these data. Use a scale of 2 cm to represent 5 hours on the \(x\)-axis and 2 cm to represent 10 points on the \(y\)-axis.
(i) \({\bar x}\), the mean number of hours spent on social media;
(ii) \({\bar y}\), the mean number of IB Diploma points.
Plot the point \((\bar x,{\text{ }}\bar y)\) on your scatter diagram and label this point M.
Write down the value of \(r\), the Pearson’s product–moment correlation coefficient, for these data.
Write down the equation of the regression line \(y\) on \(x\) for these eight male students.
Draw the regression line, from part (e), on your scatter diagram.
Use the given equation of the regression line to estimate the number of IB Diploma points that this girl obtained.
Write down a reason why this estimate is not reliable.
A survey was conducted to determine the length of time, \(t\), in minutes, people took to drink their coffee in a café. The information is shown in the following grouped frequency table.
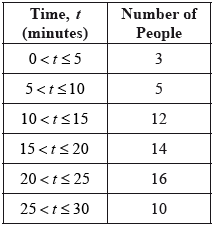
Write down the total number of people who were surveyed.
Write down the mid-interval value for the \(10 < t \leqslant 15\) group.
Find an estimate of the mean time people took to drink their coffee.
The information above has been rewritten as a cumulative frequency table.

Write down the value of \(a\) and the value of \(b\).
This information is shown in the following cumulative frequency graph.
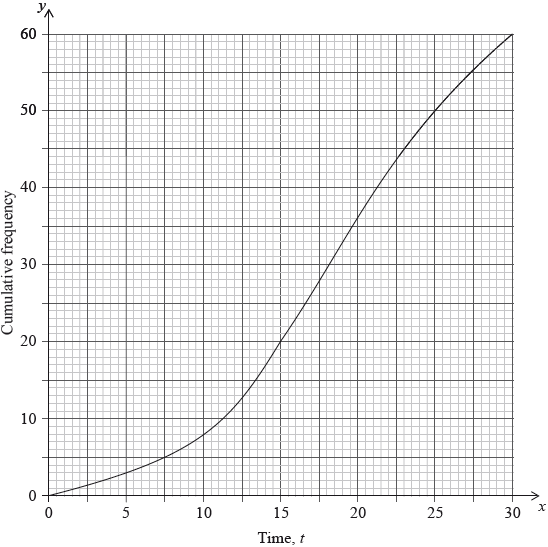
For the people who were surveyed, use the graph to estimate
(i) the time taken for the first \(40\) people to drink their coffee;
(ii) the number of people who take less than \(8\) minutes to drink their coffee;
(iii) the number of people who take more than \(23\) minutes to drink their coffee.
A group of 800 students answered 40 questions on a category of their choice out of History, Science and Literature.
For each student the category and the number of correct answers, \(N\), was recorded. The results obtained are represented in the following table.
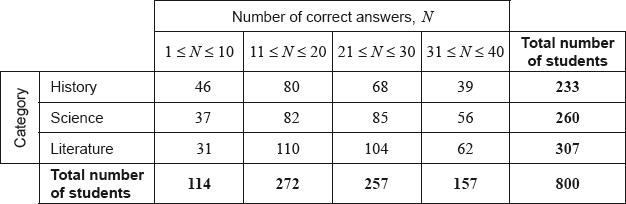
A \({\chi ^2}\) test at the 5% significance level is carried out on the results. The critical value for this test is 12.592.
State whether \(N\) is a discrete or a continuous variable.
Write down, for \(N\), the modal class;
Write down, for \(N\), the mid-interval value of the modal class.
Use your graphic display calculator to estimate the mean of \(N\);
Use your graphic display calculator to estimate the standard deviation of \(N\).
Find the expected frequency of students choosing the Science category and obtaining 31 to 40 correct answers.
Write down the null hypothesis for this test;
Write down the number of degrees of freedom.
Write down the \(p\)-value for the test;
Write down the \({\chi ^2}\) statistic.
State the result of the test. Give a reason for your answer.
The cumulative frequency graph shows the speed, \(s\), in \({\text{km}}\,{{\text{h}}^{ - 1}}\), of \(120\) vehicles passing a hospital gate.
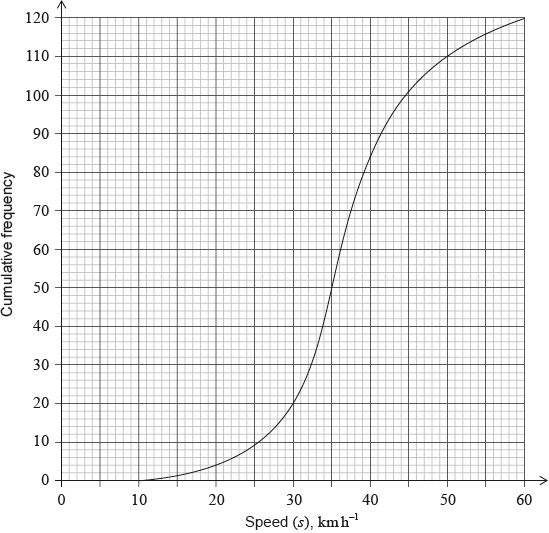
Estimate the minimum possible speed of one of these vehicles passing the hospital gate.
Find the median speed of the vehicles.
Write down the \({75^{{\text{th}}}}\) percentile.
Calculate the interquartile range.
The speed limit past the hospital gate is \(50{\text{ km}}\,{{\text{h}}^{ - 1}}\).
Find the number of these vehicles that exceed the speed limit.
The table shows the speeds of these vehicles travelling past the hospital gate.
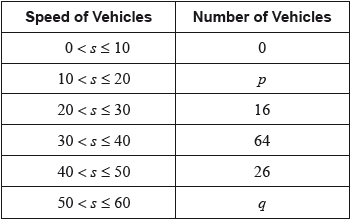
Find the value of \(p\) and of \(q\).
The table shows the speeds of these vehicles travelling past the hospital gate.

(i) Write down the modal class.
(ii) Write down the mid-interval value for this class.
The table shows the speeds of these vehicles travelling past the hospital gate.

Use your graphic display calculator to calculate an estimate of
(i) the mean speed of these vehicles;
(ii) the standard deviation.
It is proposed that the speed limit past the hospital gate is reduced to \(40{\text{ km}}\,{{\text{h}}^{ - 1}}\) from the current \(50{\text{ km}}\,{{\text{h}}^{ - 1}}\).
Find the percentage of these vehicles passing the hospital gate that do not exceed the current speed limit but would exceed the new speed limit.
The table below shows the scores for 12 golfers for their first two rounds in a local golf tournament.
(i) Write down the mean score in Round 1.
(ii) Write down the standard deviation in Round 1.
(iii) Find the number of these golfers that had a score of more than one standard deviation above the mean in Round 1.
Write down the correlation coefficient, r.
Write down the equation of the regression line of y on x.
Another golfer scored 70 in Round 1.
Calculate an estimate of his score in Round 2.
Another golfer scored 89 in Round 1.
Determine whether you can use the equation of the regression line to estimate his score in Round 2. Give a reason for your answer.
The figure below shows the lengths in centimetres of fish found in the net of a small trawler.
Find the total number of fish in the net.
Find (i) the modal length interval,
(ii) the interval containing the median length,
(iii) an estimate of the mean length.
(i) Write down an estimate for the standard deviation of the lengths.
(ii) How many fish (if any) have length greater than three standard deviations above the mean?
The fishing company must pay a fine if more than 10% of the catch have lengths less than 40cm.
Do a calculation to decide whether the company is fined.
A sample of 15 of the fish was weighed. The weight, W was plotted against length, L as shown below.
Exactly two of the following statements about the plot could be correct. Identify the two correct statements.
Note: You do not need to enter data in a GDC or to calculate r exactly.
(i) The value of r, the correlation coefficient, is approximately 0.871.
(ii) There is an exact linear relation between W and L.
(iii) The line of regression of W on L has equation W = 0.012L + 0.008 .
(iv) There is negative correlation between the length and weight.
(v) The value of r, the correlation coefficient, is approximately 0.998.
(vi) The line of regression of W on L has equation W = 63.5L + 16.5.
Daniel grows apples and chooses at random a sample of 100 apples from his harvest.
He measures the diameters of the apples to the nearest cm. The following table shows the distribution of the diameters.

Using your graphic display calculator, write down the value of
(i) the mean of the diameters in this sample;
(ii) the standard deviation of the diameters in this sample.
Daniel assumes that the diameters of all of the apples from his harvest are normally distributed with a mean of 7 cm and a standard deviation of 1.2 cm. He classifies the apples according to their diameters as shown in the following table.
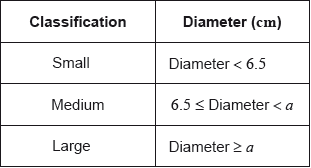
Calculate the percentage of small apples in Daniel’s harvest.
Daniel assumes that the diameters of all of the apples from his harvest are normally distributed with a mean of 7 cm and a standard deviation of 1.2 cm. He classifies the apples according to their diameters as shown in the following table.

Of the apples harvested, 5% are large apples.
Find the value of \(a\).
Daniel assumes that the diameters of all of the apples from his harvest are normally distributed with a mean of 7 cm and a standard deviation of 1.2 cm. He classifies the apples according to their diameters as shown in the following table.

Find the percentage of medium apples.
Daniel assumes that the diameters of all of the apples from his harvest are normally distributed with a mean of 7 cm and a standard deviation of 1.2 cm. He classifies the apples according to their diameters as shown in the following table.

This year, Daniel estimates that he will grow \({\text{100}}\,{\text{000}}\) apples.
Estimate the number of large apples that Daniel will grow this year.
The table shows the distance, in km, of eight regional railway stations from a city centre terminus and the price, in \($\), of a return ticket from each regional station to the terminus.

Draw a scatter diagram for the above data. Use a scale of \(1\) cm to represent \(10\) km on the \(x\)-axis and \(1\) cm to represent \(\$10\) on the \(y\)-axis.
Use your graphic display calculator to find
(i) \(\bar x\), the mean of the distances;
(ii) \(\bar y\), the mean of the prices.
Plot and label the point \({\text{M }}(\bar x,{\text{ }}\bar y)\) on your scatter diagram.
Use your graphic display calculator to find
(i) the product–moment correlation coefficient, \(r\,;\)
(ii) the equation of the regression line \(y\) on \(x\).
Draw the regression line \(y\) on \(x\) on your scatter diagram.
A ninth regional station is \(76\) km from the city centre terminus.
Use the equation of the regression line to estimate the price of a return ticket to the city centre terminus from this regional station. Give your answer correct to the nearest \({\mathbf{\$ }}\).
Give a reason why it is valid to use your regression line to estimate the price of this return ticket.
The actual price of the return ticket is \(\$80\).
Using your answer to part (f), calculate the percentage error in the estimated price of the ticket.
The lengths (\(l\)) in centimetres of \(100\) copper pipes at a local building supplier were measured. The results are listed in the table below.
Write down the mode.
Using your graphic display calculator, write down the value of
(i) the mean;
(ii) the standard deviation;
(iii) the median.
Find the interquartile range.
Draw a box and whisker diagram for this data, on graph paper, using a scale of \(1{\text{ cm}}\) to represent \(5{\text{ cm}}\).
Sam estimated the value of the mean of the measured lengths to be \(43{\text{ cm}}\).
Find the percentage error of Sam’s estimated mean.
Alex and Kris are riding their bicycles together along a bicycle trail and note the following distance markers at the given times.
Draw a scatter diagram of the data. Use 1 cm to represent 1 hour and 1 cm to represent 10 km.
Write down for this set of data the mean time, \(\bar t\).
Write down for this set of data the mean distance, \(\bar d\).
Mark and label the point \(M(\bar t,{\text{ }}\bar d)\) on your scatter diagram.
Draw the line of best fit on your scatter diagram.
Using your graph, estimate the time when Alex and Kris pass the 85 km distance marker. Give your answer correct to one decimal place.
Write down the equation of the regression line for the data given.
Using your equation calculate the distance marker passed by the cyclists at 10.3 hours.
Is this estimate of the distance reliable? Give a reason for your answer.
In a mountain region there appears to be a relationship between the number of trees growing in the region and the depth of snow in winter. A set of 10 areas was chosen, and in each area the number of trees was counted and the depth of snow measured. The results are given in the table below.
In a study on \(100\) students there seemed to be a difference between males and females in their choice of favourite car colour. The results are given in the table below. A \(\chi^2\) test was conducted.
Use your graphic display calculator to find the mean number of trees.
Use your graphic display calculator to find the mean depth of snow.
Use your graphic display calculator to find the standard deviation of the depth of snow.
The covariance, Sxy = 188.5.
Write down the product-moment correlation coefficient, r.
Write down the equation of the regression line of y on x.
If the number of trees in an area is 55, estimate the depth of snow.
Use the equation of the regression line to estimate the depth of snow in an area with 100 trees.
Decide whether the answer in (e)(i) is a valid estimate of the depth of snow in the area. Give a reason for your answer.
Write down the total number of male students.
Show that the expected frequency for males, whose favourite car colour is blue, is 12.6.
The calculated value of \({\chi ^2}\) is \(1.367\) and the critical value of \({\chi ^2}\) is \(5.99\) at the \(5\%\) significance level.
Write down the null hypothesis for this test.
The calculated value of \({\chi ^2}\) is \(1.367\) and the critical value of \({\chi ^2}\) is \(5.99\) at the \(5\%\) significance level.
Write down the number of degrees of freedom.
The calculated value of \({\chi ^2}\) is \(1.367\) and the critical value of \({\chi ^2}\) is \(5.99\) at the \(5\%\) significance level.
Determine whether the null hypothesis should be accepted at the \(5\%\) significance level. Give a reason for your answer.
The number of bottles of water sold at a railway station on each day is given in the following table.
Write down
(i) the mean temperature;
(ii) the standard deviation of the temperatures.
Write down the correlation coefficient, \(r\), for the variables \(n\) and \(T\).
Comment on your value for \(r\).
The equation of the line of regression for \(n\) on \(T\) is \(n = dT - 100\).
(i) Write down the value of \(d\).
(ii) Estimate how many bottles of water will be sold when the temperature is \({19.6^ \circ }\).
On a day when the temperature was \({36^ \circ }\) Peter calculates that \(314\) bottles would be sold. Give one reason why his answer might be unreliable.
The diagram shows the cumulative frequency graph for the time t taken to perform a certain task by 2000 men.
Use the diagram to estimate the median time.
Use the diagram to estimate the upper quartile and the lower quartile.
Use the diagram to estimate the interquartile range.
Find the number of men who take more than 11 seconds to perform the task.
55 % of the men took less than p seconds to perform the task. Find p.
The times taken for the 2000 men were grouped as shown in the table below.
Write down the value of a.
The times taken for the 2000 men were grouped as shown in the table below.
Write down the value of b.
Use your graphic display calculator to find an estimate of the mean time.
Use your graphic display calculator to find an estimate of the standard deviation of the time.
Everyone who performs the task in less than one standard deviation below the mean will receive a bonus. Pedro takes 9.5 seconds to perform the task.
Does Pedro receive the bonus? Justify your answer.
On one day 180 flights arrived at a particular airport. The distance travelled and the arrival status for each incoming flight was recorded. The flight was then classified as on time, slightly delayed, or heavily delayed.
The results are shown in the following table.
A χ2 test is carried out at the 10 % significance level to determine whether the arrival status of incoming flights is independent of the distance travelled.
The critical value for this test is 7.779.
A flight is chosen at random from the 180 recorded flights.
State the alternative hypothesis.
Calculate the expected frequency of flights travelling at most 500 km and arriving slightly delayed.
Write down the number of degrees of freedom.
Write down the χ2 statistic.
Write down the associated p-value.
State, with a reason, whether you would reject the null hypothesis.
Write down the probability that this flight arrived on time.
Given that this flight was not heavily delayed, find the probability that it travelled between 500 km and 5000 km.
Two flights are chosen at random from those which were slightly delayed.
Find the probability that each of these flights travelled at least 5000 km.
A random sample of 167 people who own mobile phones was used to collect data on the amount of time they spent per day using their phones. The results are displayed in the table below.
Manuel conducts a survey on a random sample of 751 people to see which television programme type they watch most from the following: Drama, Comedy, Film, News. The results are as follows.
Manuel decides to ignore the ages and to test at the 5 % level of significance whether the most watched programme type is independent of gender.
State the modal group.
Use your graphic display calculator to calculate approximate values of the mean and standard deviation of the time spent per day on these mobile phones.
On graph paper, draw a fully labelled histogram to represent the data.
Draw a table with 2 rows and 4 columns of data so that Manuel can perform a chi-squared test.
State Manuel’s null hypothesis and alternative hypothesis.
Find the expected frequency for the number of females who had ‘Comedy’ as their most-watched programme type. Give your answer to the nearest whole number.
Using your graphic display calculator, or otherwise, find the chi-squared statistic for Manuel’s data.
(i) State the number of degrees of freedom available for this calculation.
(ii) State his conclusion.
The speed, \(s\) , in \({\text{km }}{{\text{h}}^{ - 1}}\), of \(120\) vehicles passing a point on the road was measured. The results are given below.
Write down the midpoint of the \(60 < s \leqslant 70\) interval.
Use your graphic display calculator to find an estimate for
(i) the mean speed of the vehicles;
(ii) the standard deviation of the speeds of the vehicles.
Write down the number of vehicles whose speed is less than or equal to \({\text{60 km }}{{\text{h}}^{ - 1}}\).
Consider the cumulative frequency table below.
Write down the value of \(a\) , of \(b\) and of \(c\) .
Consider the cumulative frequency table below.
Draw a cumulative frequency graph for the information from the table. Use \(1\) cm to represent \({\text{10 km }}{{\text{h}}^{ - 1}}\) on the horizontal axis and \(1\) cm to represent \(10\) vehicles on the vertical axis.
Use your cumulative frequency graph to estimate
(i) the median speed of the vehicles;
(ii) the number of vehicles that are travelling at a speed less than or equal to \({\text{65 km }}{{\text{h}}^{ - 1}}\).
All drivers whose vehicle’s speed is greater than one standard deviation above the speed limit of \({\text{50 km }}{{\text{h}}^{ - 1}}\) will be fined.
Use your graph to estimate the number of drivers who will be fined.
Francesca is a chef in a restaurant. She cooks eight chickens and records their masses and cooking times. The mass m of each chicken, in kg, and its cooking time t, in minutes, are shown in the following table.
Draw a scatter diagram to show the relationship between the mass of a chicken and its cooking time. Use 2 cm to represent 0.5 kg on the horizontal axis and 1 cm to represent 10 minutes on the vertical axis.
Write down for this set of data
(i) the mean mass, \(\bar m\) ;
(ii) the mean cooking time, \(\bar t\) .
Label the point \({\text{M}}(\bar m,\bar t)\) on the scatter diagram.
Draw the line of best fit on the scatter diagram.
Using your line of best fit, estimate the cooking time, in minutes, for a 1.7 kg chicken.
Write down the Pearson’s product–moment correlation coefficient, r .
Using your value for r , comment on the correlation.
The cooking time of an additional 2.0 kg chicken is recorded. If the mass and cooking time of this chicken is included in the data, the correlation is weak.
(i) Explain how the cooking time of this additional chicken might differ from that of the other eight chickens.
(ii) Explain how a new line of best fit might differ from that drawn in part (d).
Part A
A university required all Science students to study one language for one year. A survey was carried out at the university amongst the 150 Science students. These students all studied one of either French, Spanish or Russian. The results of the survey are shown below.
Ludmila decides to use the \({\chi ^2}\) test at the \(5\% \) level of significance to determine whether the choice of language is independent of gender.
At the end of the year, only seven of the female Science students sat examinations in Science and French. The marks for these seven students are shown in the following table.
State Ludmila’s null hypothesis.
Write down the number of degrees of freedom.
Find the expected frequency for the females studying Spanish.
Use your graphic display calculator to find the \({\chi ^2}\) test statistic for this data.
State whether Ludmila accepts the null hypothesis. Give a reason for your answer.
Draw a labelled scatter diagram for this data. Use a scale of \(2{\text{ cm}}\) to represent \(10{\text{ marks}}\) on the \(x\)-axis (\(S\)) and \(10{\text{ marks}}\) on the \(y\)-axis (\(F\)).
Use your graphic calculator to find
(i) \({\bar S}\), the mean of \(S\) ;
(ii) \({\bar F}\), the mean of \(F\) .
Plot the point \({\text{M}}(\bar S{\text{, }}\bar F)\) on your scatter diagram.
Use your graphic display calculator to find the equation of the regression line of \(F\) on \(S\) .
Draw the regression line on your scatter diagram.
Carletta’s mark on the Science examination was \(44\). She did not sit the French examination.
Estimate Carletta’s mark for the French examination.
Monique’s mark on the Science examination was 85. She did not sit the French examination. Her French teacher wants to use the regression line to estimate Monique’s mark.
State whether the mark obtained from the regression line for Monique’s French examination is reliable. Justify your answer.
The diagram below shows a square based right pyramid. ABCD is a square of side 10 cm. VX is the perpendicular height of 8 cm. M is the midpoint of BC.
In a mountain region there appears to be a relationship between the number of trees growing in the region and the depth of snow in winter. A set of 10 areas was chosen, and in each area the number of trees was counted and the depth of snow measured. The results are given in the table below.
A path goes around a forest so that it forms the three sides of a triangle. The lengths of two sides are 550 m and 290 m. These two sides meet at an angle of 115°. A diagram is shown below.
Write down the length of XM.
Use your graphic display calculator to find the standard deviation of the number of trees.
Calculate the length of VM.
Calculate the angle between VM and ABCD.
Calculate the length of the third side of the triangle. Give your answer correct to the nearest 10 m.
Calculate the area enclosed by the path that goes around the forest.
Inside the forest a second path forms the three sides of another triangle named ABC. Angle BAC is 53°, AC is 180 m and BC is 230 m.
Calculate the size of angle ACB.
For an ecological study, Ernesto measured the average concentration \((y)\) of the fine dust, \({\text{PM}}10\), in the air at different distances \((x)\) from a power plant. His data are represented on the following scatter diagram. The concentration of \({\text{PM}}10\) is measured in micrograms per cubic metre and the distance is measured in kilometres.
His data are also listed in the following table.
Use the scatter diagram to find the value of \(a\) and of \(b\) in the table.
Calculate
i) \({\bar x}\) , the mean distance from the power plant;
ii) \({\bar y}\) , the mean concentration of \({\text{PM}}10\) ;
iii) \(r\) , the Pearson’s product–moment correlation coefficient.
Write down the equation of the regression line \(y\) on \(x\) .
Ernesto’s school is located \(14\,{\text{km}}\) from the power plant. He uses the equation of the regression line to estimate the concentration of \({\text{PM}}10\) in the air at his school.
i) Calculate the value of Ernesto’s estimate.
ii) State whether Ernesto’s estimate is reliable. Justify your answer.
A transportation company owns 30 buses. The distance that each bus has travelled since being purchased by the company is recorded. The cumulative frequency curve for these data is shown.
It is known that 8 buses travelled more than m kilometres.
Find the number of buses that travelled a distance between 15000 and 20000 kilometres.
Use the cumulative frequency curve to find the median distance.
Use the cumulative frequency curve to find the lower quartile.
Use the cumulative frequency curve to find the upper quartile.
Hence write down the interquartile range.
Write down the percentage of buses that travelled a distance greater than the upper quartile.
Find the number of buses that travelled a distance less than or equal to 12 000 km.
Find the value of m.
The smallest distance travelled by one of the buses was 2500 km.
The longest distance travelled by one of the buses was 23 000 km.
On graph paper, draw a box-and-whisker diagram for these data. Use a scale of 2 cm to represent 5000 km.
The heat output in thermal units from burning \(1{\text{ kg}}\) of wood changes according to the wood’s percentage moisture content. The moisture content and heat output of \(10\) blocks of the same type of wood each weighing \(1{\text{ kg}}\) were measured. These are shown in the table.
Draw a scatter diagram to show the above data. Use a scale of \(2{\text{ cm}}\) to represent \(10\% \) on the x-axis and a scale of \(2{\text{ cm}}\) to represent \(10\) thermal units on the y-axis.
Write down
(i) the mean percentage moisture content, \(\bar x\) ;
(ii) the mean heat output, \(\bar y\) .
Plot the point \((\bar x{\text{, }}\bar y)\) on your scatter diagram and label this point M .
Write down the product-moment correlation coefficient, \(r\) .
The equation of the regression line \(y\) on \(x\) is \(y = - 0.470x + 83.7\) . Draw the regression line \(y\) on \(x\) on your scatter diagram.
The equation of the regression line \(y\) on \(x\) is \(y = - 0.470x + 83.7\) . Estimate the heat output in thermal units of a \(1{\text{ kg}}\) block of wood that has \(25\% \) moisture content.
The equation of the regression line \(y\) on \(x\) is \(y = - 0.470x + 83.7\) . State, with a reason, whether it is appropriate to use the regression line \(y\) on \(x\) to estimate the heat output in part (f).
In an environmental study of plant diversity around a lake, a biologist collected data about the number of different plant species (y) that were growing at different distances (x) in metres from the lake shore.
Draw a scatter diagram to show the data. Use a scale of 2 cm to represent 10 metres on the x-axis and 2 cm to represent 10 plant species on the y-axis.
Using your scatter diagram, describe the correlation between the number of different plant species and the distance from the lake shore.
Use your graphic display calculator to write down \(\bar x\), the mean of the distances from the lake shore.
Use your graphic display calculator to write down \(\bar y\), the mean number of plant species.
Plot the point (\(\bar x\), \(\bar y\)) on your scatter diagram. Label this point M.
Write down the equation of the regression line y on x for the above data.
Draw the regression line y on x on your scatter diagram.
Estimate the number of plant species growing 30 metres from the lake shore.
200 people were asked the amount of time T (minutes) they had spent in the supermarket. The results are represented in the table below.
State if the data is discrete or continuous.
State the modal group.
Write down the midpoint of the interval 10 < T ≤ 20 .
Use your graphic display calculator to find an estimate for
(i) the mean;
(ii) the standard deviation.
The results are represented in the cumulative frequency table below, with upper class boundaries of 10, 20, 30, 40, 50.
Write down the value of
(i) q;
(ii) r.
The results are represented in the cumulative frequency table below, with upper class boundaries of 10, 20, 30, 40, 50.
On graph paper, draw a cumulative frequency graph, using a scale of 2 cm to represent 10 minutes (T) on the horizontal axis and 1 cm to represent 10 people on the vertical axis.
Use your graph from part (f) to estimate
(i) the median;
(ii) the 90th percentile of the results;
(iii) the number of people who shopped at the supermarket for more than 15 minutes.